About
The Art of Symmetry - Structured Beauty in Nature
To many of us, whenever someone mentions the word "symmetry", the first thing that comes to mind is some shape that looks the same when reflected in a mirror. To some, yet another thing that comes to mind would be some form of balance and harmony, like the Yin and Yang of Taoist culture.

Symmetry is a property of objects best described in the mathematical lingo as "the property of staying invariant under some action". Those are big words, so let us try to break down what they intuitively mean. The word "invariant" is just a fancy, more technical term for "unchanged", and in mathematics, the word "action" can be thought of as something like a reflection, a rotation, a translation, et cetera.
In other words, symmetry simply refers to the property of some object being unchanged by some reflection, rotation or translation (there is more subtlety and is much more general than that, but we will not go there as it is beyond the scope of this text). Take a moment to ponder this interpretation of what symmetry means, and try to imagine how this does indeed capture the intuition that we have regarding symmetrical objects.

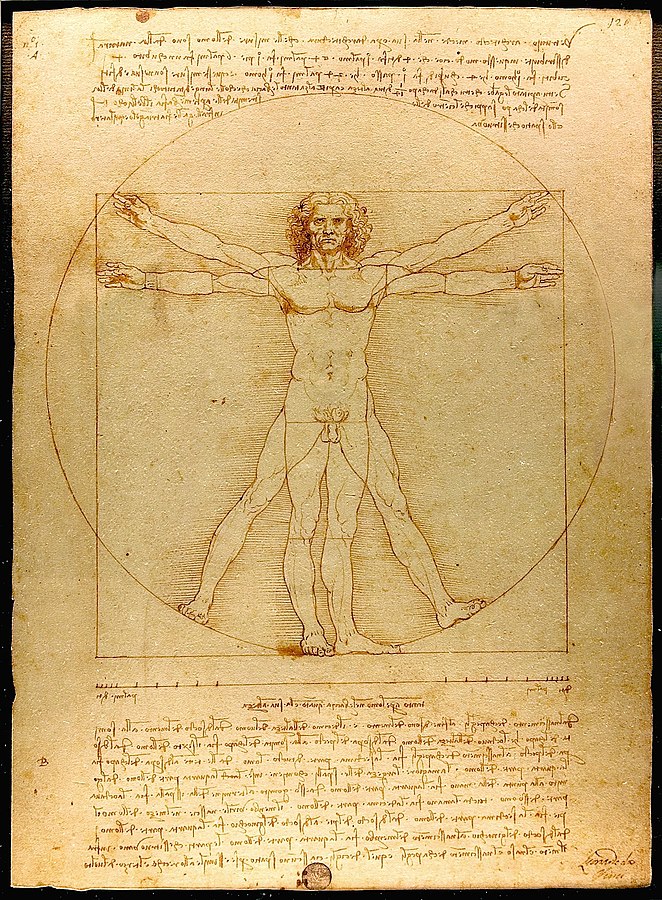
As the title of this chapter implies, symmetry is seen as a form of art, and is found everywhere in nature. Look around you, and you can see symmetries in flowers, the moon, and in the appearances of many animals. In fact, humans are mostly symmetric too! The famous Italian polymath Leonardo da Vinci was well-known for drawing the Vitruvian Man, what he thought was the ideal proportions of the human body. One thing that stands out in the Vitruvian Man is the high level of symmetry, which says a lot about how symmetry is viewed as an ideal form of beauty in society. Think about it, we humans tend to see other people as more beautiful and attractive if their faces and bodies are symmetric.
Symmetry shows up all the time in architecture as well, with the Taj Mahal and the Islamic design of mosques being prime examples of buildings with very symmetrical designs. It would be no surprise that we humans use the same measure of symmetry to judge the beauty of both buildings and other living things. After all, there is some elegance to symmetry, no?

Well, at this point, we are getting ahead of ourselves. All this talk about symmetry, and we still have not actually discussed what exactly it is we are talking about. Without further ado, let us then proceed to the first chapter.
Chapter 1: Mirror Mirror On The Wall, Who Is The Most Symmetrical Of Them All?
A vain queen strolls down the steps of her castle, down into the deep, dark dungeon. Entering her own private workshop, she dusted off a tall object draped in a shabby cloth, and with a well-practiced flourish, pulled the cloth away to reveal a beautiful mirror.
"Mirror Mirror on the wall."
The screen of the mirror suddenly sprung to life, the various colors of smoke coming together in harmony to form a rainbow-colored mask. Three holes cut themselves into the mask of smoke, forming what appeared to be a very simplified face.
"How may I help you today, my queen?"
The queen, unshaken by this colorful display in front of her, coldly replied with a line that she must have said many times before.
"Who is the most symmetrical of them all?"
"Of course, it is you, my queen."
Now, the magic mirror did not believe one bit of what it said, of course. Being based off an object that is designed to look the same in mirror reflections, it is clearly much more symmetrical than the human-shaped queen. However, she is the queen of the land, and the mirror is bound to her service, and so it must satisfy her.
Satisfied with the day's answer, the queen left the dungeons, leaving the mirror to its own thoughts. It was troubled by the recent appearance of several, more symmetric beings in the kingdom, and seeing that the queen did not enjoy the presence of beings more symmetrical than herself, the mirror did not know what to tell the queen.
The next day, the queen descended into the dungeon again, and asked the same question as she had always asked for the past many years.
"Mirror Mirror on the wall, who is the most symmetrical of them all?"
This time, the mirror hesitated. This behavior was most strange, for the mirror usually replies in an instant.
"Of course you are a very symmetrical being, my queen. But..." the mirror seemed troubled, "there have appeared beings who are more symmetrical than you are, my queen."
Upon hearing this, the air around the vain queen shifted. In a fit of silent rage, she swiftly left the dungeon, back into her throne room. She summoned the foreign, supposedly more symmetrical beings to her castle the next day.
"Hear me, foreign ones. I am the queen of this land, most symmetrical of all."
The entourage of strange beings, whose shapes were not humanoid in the least, simply remained where they were, completely unfazed by the regal display before them.
"I will not allow beings who are more symmetrical than I to stay in my kingdom. But I am a fair ruler, and I shall give you all one chance to prove the extent of your symmetry."
The queen then motioned to a member of her court to step forward.
"Now come before the judge, foreign beings, and prove to everyone else your lack of symmetry!"
In the following simulation, we shall explore the concept of reflection symmetry.
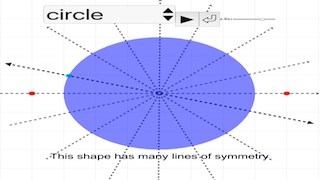
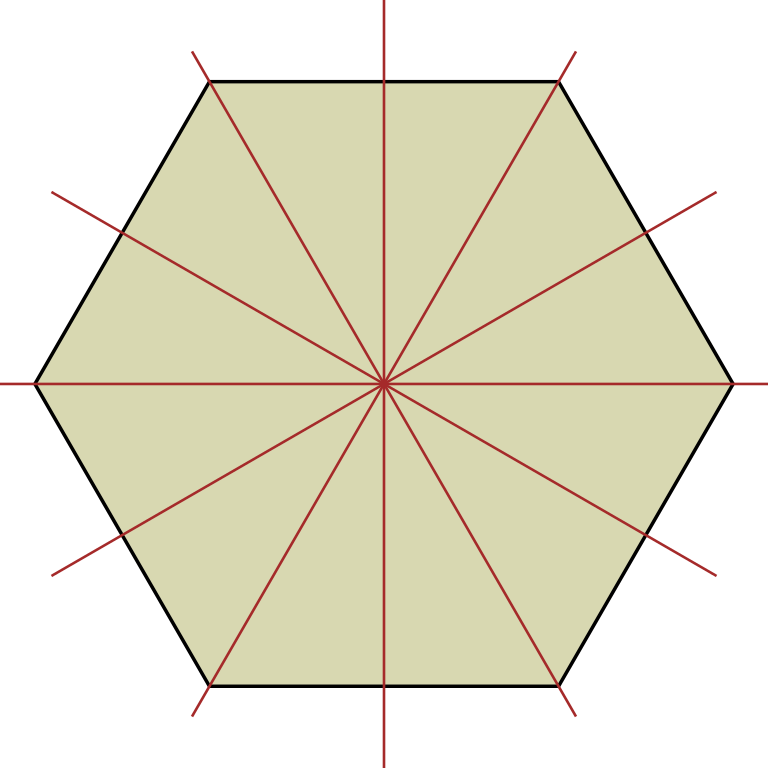
Objects which have reflection symmetry have this special thing called a line of symmetry. Simply put, a line of symmetry is a line with the property that if you cut or fold the object along the line, the resulting two halves are exactly mirror images of each other. Another way to describe a line of symmetry, keeping with our theme of mirrors in this chapter, is that a mirror which reflects an object across its line of symmetry will leave the object looking exactly the same, as if it has never been reflected.
Of course, there is nothing stopping an object from having multiple lines of symmetry. In fact, as we will see later, we can find objects with as many lines of symmetry as we want!
The foreign beings, whose bodies take the form of various shapes, line up one by one in front of you to check how symmetric they are. You, as the judge, will try to determine if they have reflection symmetry or not, and if so, how many lines of symmetry they have. Fret not, the queen has patience, and will wait for as long as you need to conduct the check. Have fun!
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits


 This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente
This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente
end faq
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
https://www.youtube.com/watch?v=I36-bO_NzEk
Version:
- http://weelookang.blogspot.sg/2017/11/symmetry-shape-javascript-html5-applet.html
- https://weelookang.blogspot.com/2021/11/symmetry-shape-javascript-html5-applet.html
Other Resources