About
Javelin throwing: The search for optimal distance
Phillip Wall and Wolfgang Christian
JavaScript version by loo kang
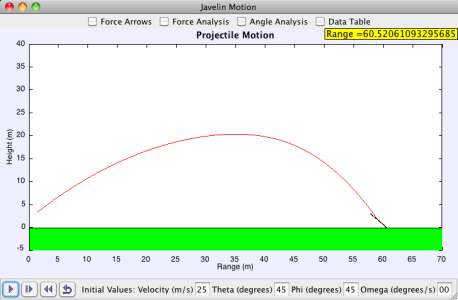
This model simulates the throw of a javelin with no spin and no wind in a vertical plane. This is a simplified situaiton to be able to analyze the pure dynamics of a javelin throw. The user can change several initial conditions including velocity, angle of the javelin (theta), angle of the velocity vector (phi), angle of attack (phi), and angular velocity (omega). The user can set initial conditions and press play to see how the javelin reacts and behaves in flight. To eliminate certain conditions that produce either negative distances or errors during computation, the range for theta and phi are slightly limited. This is because we are looking for conditions that produce the farthest throws. So short throws are not as interesting in this instance.
The user may also view certain properties of the javelin's flight. Several check boxes appear on the top of the main frame with specific options. The "Force Arrows" box shows the force arrows on the javelin and how the direction and magnitude change as the flight unfolds. The red-tipped arrow is the drag force while the blue-tipped arrow is the lift force. The "Force Analysis" check box makes a plot of the magnitude of the drag and lift forces appear. The "Angle Analysis" check box produces a frame with multiple plots embedded in several radio buttons. This frame allows the user to view how the different values (theta, phi, alpha, omega, and the angular acceleration) change as the flight unfolds. Finally, the "Data Table" check box produces a table that stores helpful values after every javelin flight to compare different initial conditions.
This model gives the user the chance to try and find the optimal conditions for certain initial velocities. Reasonable initial velocities are in the range of 20-30 m/s for novices and Olympic athletes alike. Once the user finds the optimal conditions with 0 deg/s for the initial angular velocity, the user can increase the angular velocity and try to find optimal conditions again to see how they change.
There is a supplementary model with a sole purpose of computing the range as a function of inital theta and phi for different initial velocities and omegas. A pdf of a report investigating the consequences of this model is provided by the pdf button in the main frame.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
![]()

Wolfgang Christian - Davidson College; Phillip Wall; lookang
end faq
Sample Learning Goals
[text]
For Teachers
[text]
Research
[text]
Video
[text]
Version
- https://weelookang.blogspot.com/2020/02/javelin-flight-dynamics-javascript.html
- https://www.compadre.org/osp/items/detail.cfm?ID=12110 by Phillip Wall, Wolfgang Christian
Question 1: A student claims that increasing the angular velocity would increase the range of the javelin. True or false?
False. Increasing the angular velocity reduces the range.
Question 2: If a javelin thrower wants to beat the current school record of 30m, will his current conditions (initial height of release=2, initial velocity=20, theta=45, phi=45, omega=0) be able to beat the record?
Yes. Range for these conditions is 36.7m
Question 3: How does changing the initial height of release affect the time of flight? Explain your answer.
An increase in initial height of release results in increased time of flight as the javelin takes a longer time to reach the ground at height=0m.
Other Resources
[text]


.png
)




