About
1.5 Example of investigate the motion of an oscillator using experimental and graphical methods
1.5.1.Q1: what is the maximum angle of release before the motion is not accurately described as a simple harmonic motion for the case of a simple free pendulum?
Example 1: Simple pendulum A pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion
1.5.2 Suggested Inquiry Steps:
- Define the question in your own words
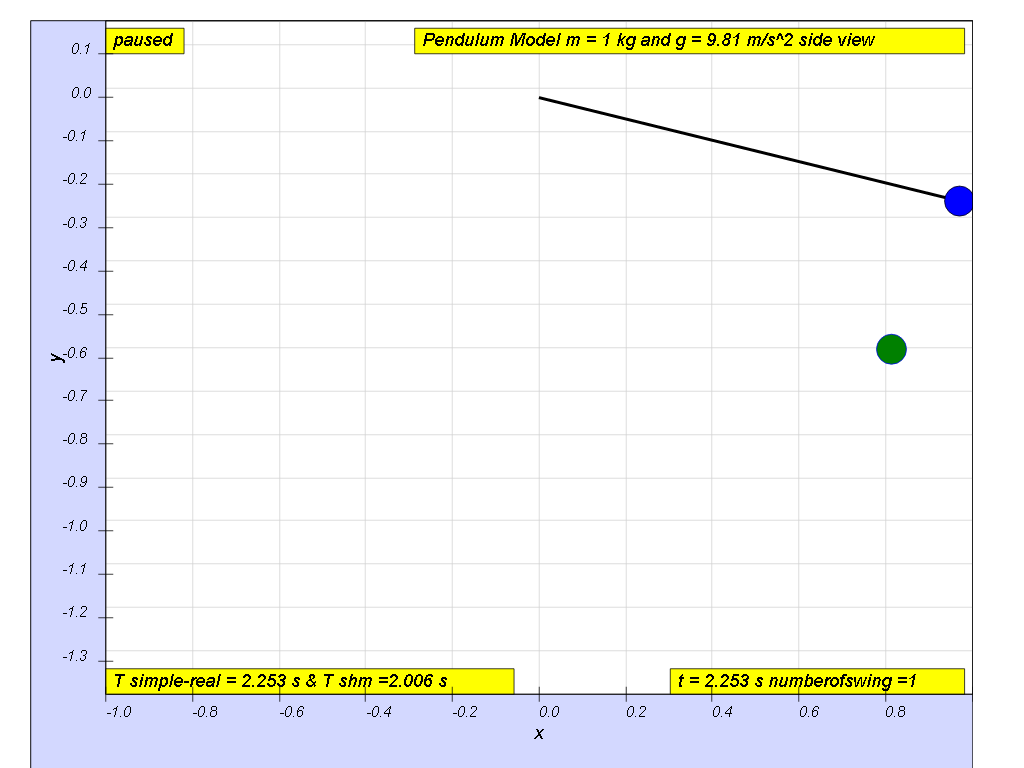
- Plan an investigation to explore angle of release to record the actual period T and theoretical period where L is the length of the mass pendulum of mass, m and g is the gravitational acceleration of which the mass is experiencing, on Earth's surface g = 9.81 m/s2
- A suggested record of the results could look like this
| angle / degree | T /s | Ttheory / s | |
| 05 | |||
| 10 | |||
| 15 | |||
| 20 | |||
| 30 | |||
| 40 | |||
| 50 | |||
| 60 | |||
| 70 | |||
| 80 | |||
| 90 |
With the evidences collected or otherwise, suggests what the conditions of which the angle of oscillation can the actual period T be approximated to theoretical period such that T ≈
1.5.3 Suggested Answer 1:
angle θ ≈ 10 degrees for , depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical.
1.5.4 Conclusion:
Motion approximates simple harmonic motion when the angle of oscillation is small < 10 degrees..
1.5.5 Other Interesting fact(s):
Motion approximates SHM when the spring does not exceed limit of proportionality during oscillations.
1.5.6 Real Life Application of Small Angle Approximations:
Astronomical applications of the Small Angle Approximation
1.5.7 YouTube
http://youtu.be/BRbCW2MsL94?t=2m16s This video shows many pendulums that goes in phase and out of phase with each other pendulum to creating a visually stunning effect.
1.5.8 Model:
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Software Requirements
| Android | iOS | Windows | MacOS | |
| with best with | Chrome | Chrome | Chrome | Chrome |
| support full-screen? | Yes. Chrome/Opera No. Firefox/ Samsung Internet | Not yet | Yes | Yes |
| cannot work on | some mobile browser that don't understand JavaScript such as..... | cannot work on Internet Explorer 9 and below |
Credits
 This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
end faq
Apps
https://play.google.com/store/apps/details?id=com.ionicframework.shm195app415781&hl=en