EJSS simple harmonic motion model with
based on models and ideas by
 |
| EJSS simple harmonic motion model
with x vs t, v vs t and a vs t graphs showing all 3
graphs https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMxva/SHMxva_Simulation.html source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMxva.zip author: lookang author of EJSS 5.0 Francisco Esquembre |
- lookang http://weelookang.blogspot.sg/2010/06/ejs-open-source-simple-harmonic-motion.html?q=SHM
- Wolfgang Christian and Francisco Esquembre http://www.opensourcephysics.org/items/detail.cfm?ID=13103
 |
| EJSS
simple harmonic motion model with x vs t, v vs t and a
vs t graphs showing all 3 graphs https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMxva/SHMxva_Simulation.html source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMxva.zip author: lookang author of EJSS 5.0 Francisco Esquembre |
The equations that model the motion of the spring mass system are:
where
Thus, this model assumes
where the terms
What is SHM?
Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. In order for simple harmonic motion to take place, the net force of the object at the end of the pendulum must be proportional to the displacement. In other words, oscillations are periodic variations in the value of a physical quantity about a central or equilibrium value.As long as the system has no energy loss, the mass will continue to oscillate. Thus, simple harmonic motion is a type of periodic motion.
Types of Oscillations:
Free oscillations
Free oscillations occur when a system is disturbed
momentarily and then allowed to move without restraint. In
the absence of damping caused by friction and viscous
forces like air drag force, free
oscillations will last forever.
Damped oscillations
Damped oscillations are free oscillations that decay with
time as a result of frictional and viscous forces.
Forced oscillations
Forced oscillations are oscillations that are subjected to a
periodic driving force provided by an external agent such as
motor or a push by a person etc.
Resonance is an interesting phenomenon that occurs when
driving force frequency matches that of the system's natural
oscillating frequency resulting in a motion that reaches
some maximum amplitude.
Definition of SHM:
A periodic motion where the acceleration a of an object is always directed towards a fixed equilibrium position and is proportional to its displacement x from that fixed point.If motion starts at the equilibrium position and starts to move to the positive direction solutions to the defining equation are:
 |
| motion starts at the
equilibrium position and starts to move to the
positive direction, defining equation follows |
 |
| motion starts at the
equilibrium position and starts to move to the
positive direction, defining equation follows |
 |
| motion starts at the
equilibrium position and starts to move to the
positive direction, defining equation follows |
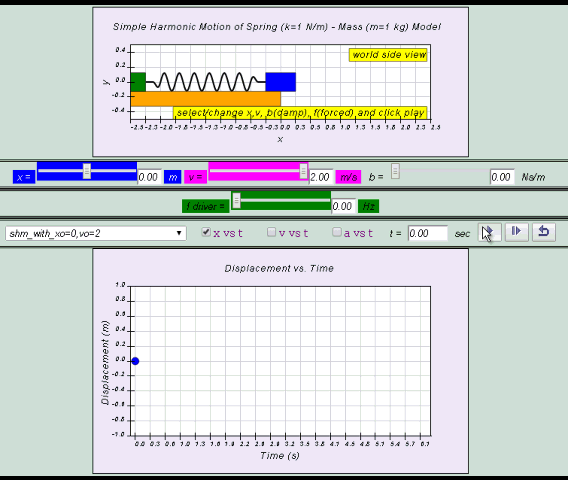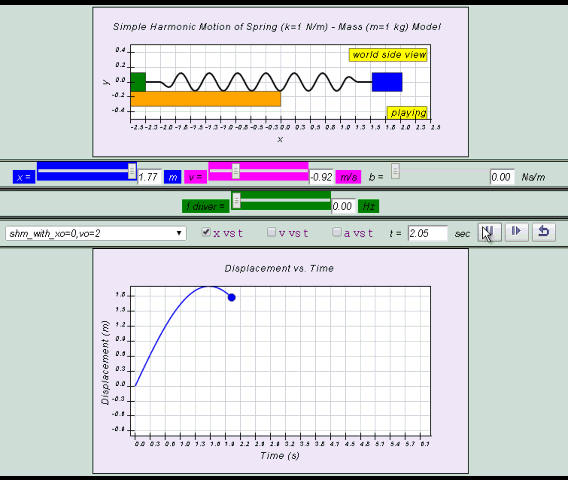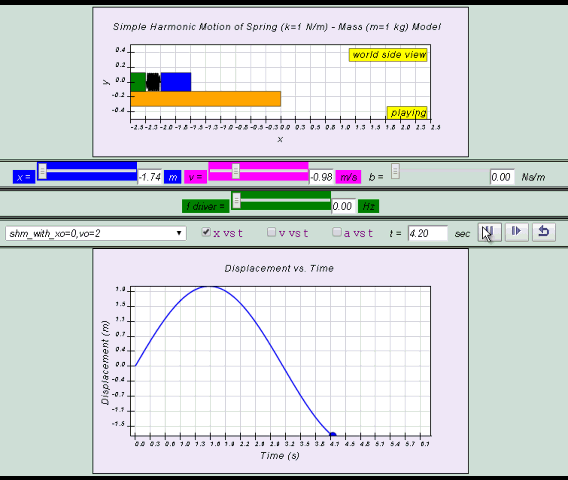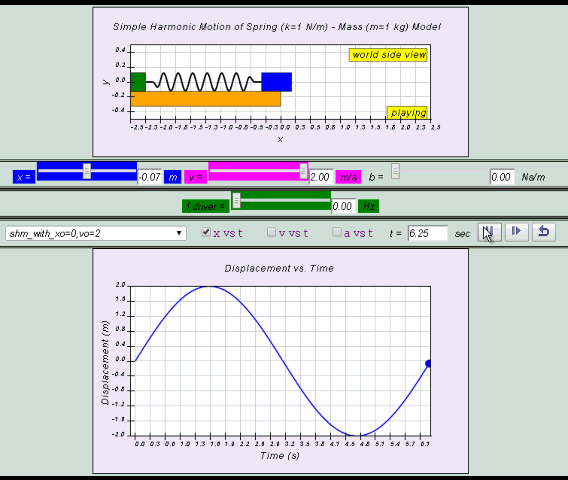
The variation with time of x, v and a seen together
graphically is as follows:
Note that
(1) the velocity of the body is deduced from the gradient of the x-t (displacement-time) graph and
(2) the acceleration of the body is deduced from the gradient of the v-t (velocity-time) graph.
x=−xocos(ωt)=xosin(ωt−π2)
v=xoωsin(ωt)=xoωcos(ωt−π2)
a=xoω2cos(ωt)=−xoω2sin(ωt−π2)
therefore , in general:
x=xosin(ωt−ϕ)
v=xoωcos(ωt−ϕ)
a=−xoω2sin(ωt−ϕ)
Note that
(1) the velocity of the body is deduced from the gradient of the x-t (displacement-time) graph and
(2) the acceleration of the body is deduced from the gradient of the v-t (velocity-time) graph.
If the motion starts to the negative amplitude position:
 |
| motion
starts at the negative position and starts to move
to the positive direction, defining equation
follows |
 |
| motion
starts at the negative position and starts to move
to the positive direction, defining equation
follows |
 |
| motion
starts at the negative position and starts to move
to the positive direction, defining equation follows
|
therefore , in general:
Damping:
If no frictional forces act on an oscillator (e.g.
simple pendulum system, mass-spring system, etc.), then
it will oscillate indefinitely.
In practice, the amplitude of the oscillations decreases
to zero as a result of friction. This type of motion is
called damped harmonic motion. Often the friction arises
from air resistance (external damping) or internal
forces (internal damping).
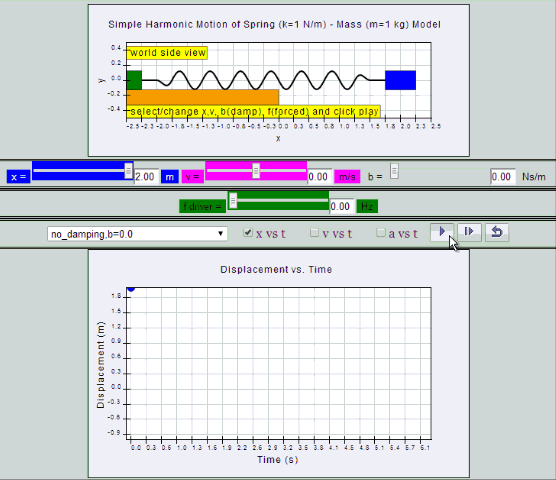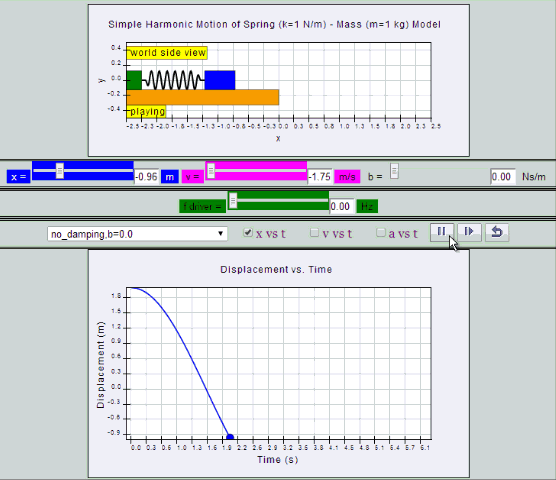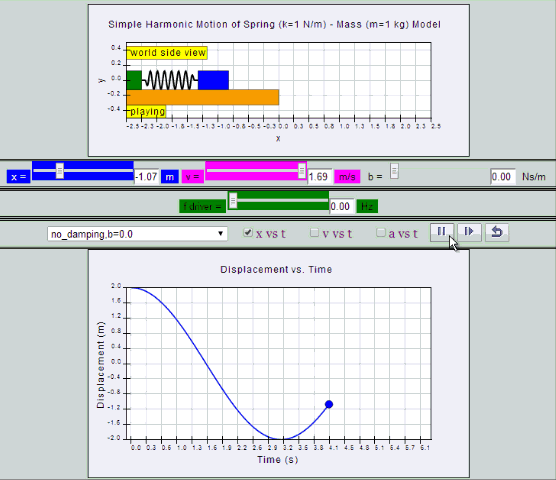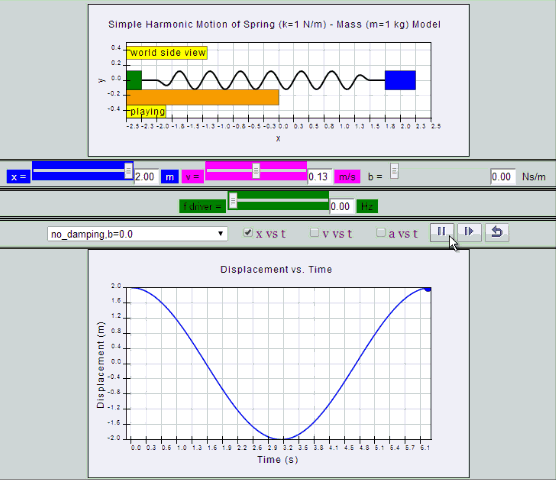
No Damping:
System oscillates forever without coming to rest.
Amplitude and thus total energy is constant.
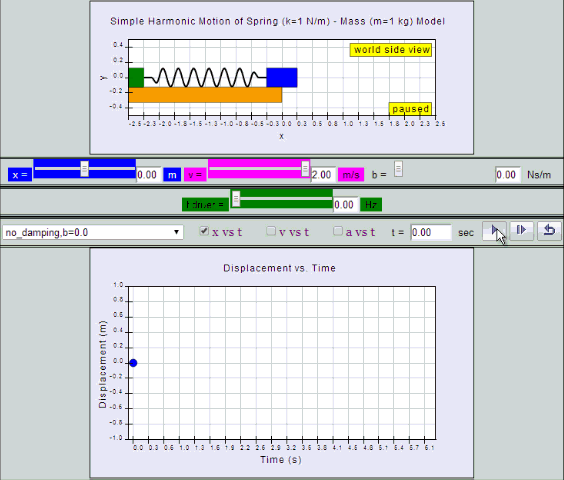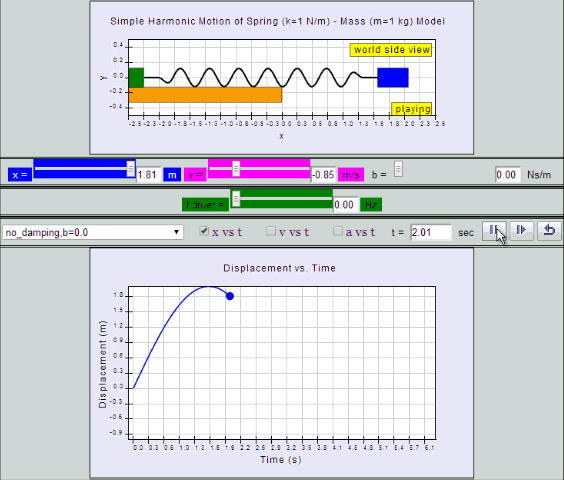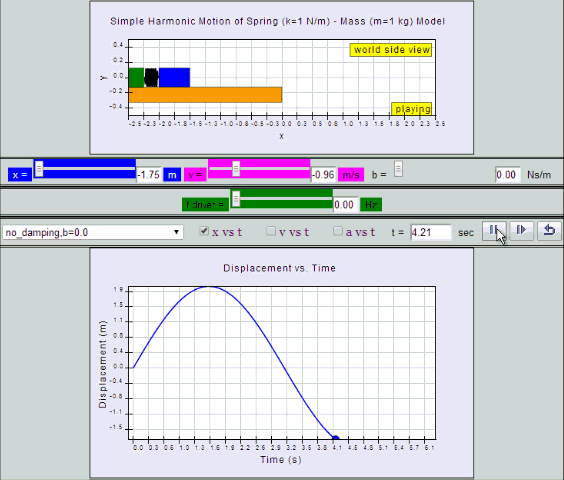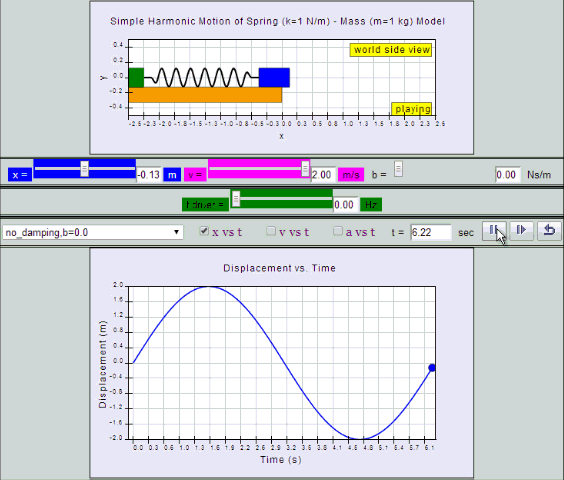 |
| no
damping, b =0, SHM starts at equilibrium position
|
 |
| no
damping, b =0, SHM starts at position |
 |
| no
damping, b =0, SHM starts at position |
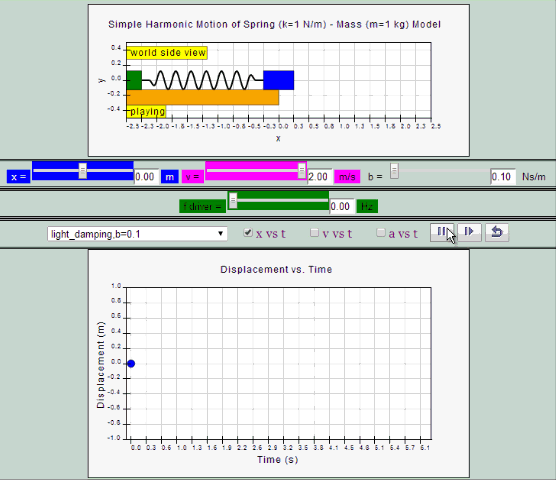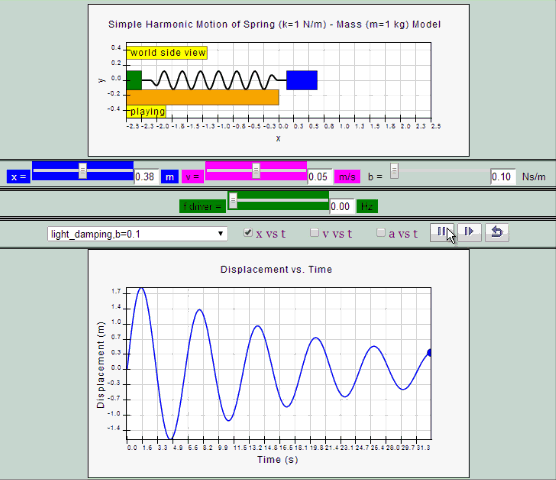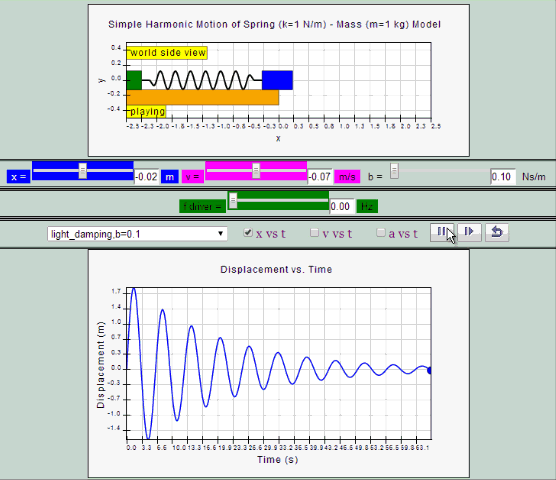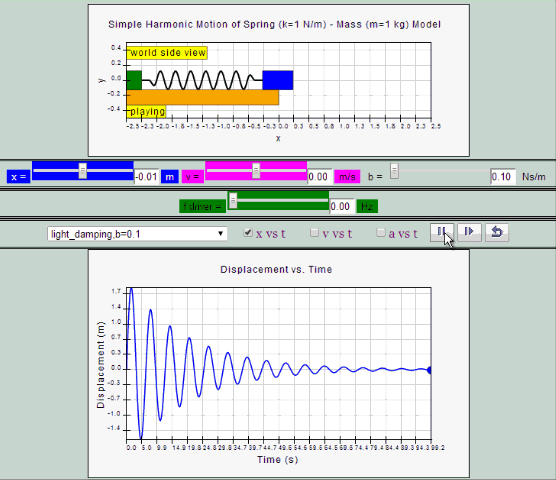
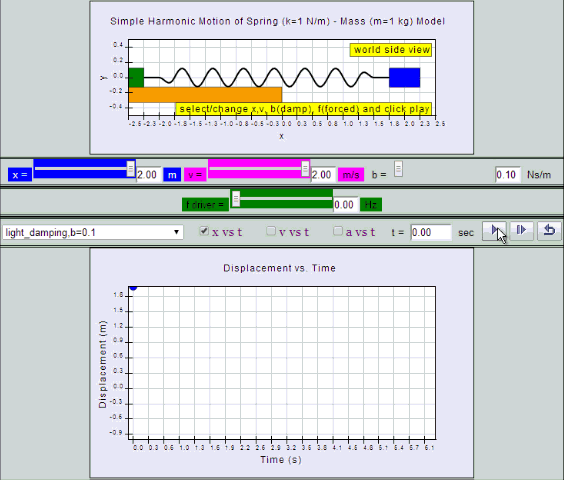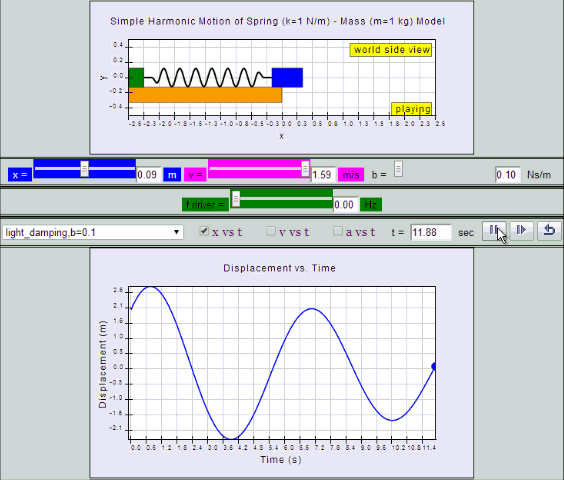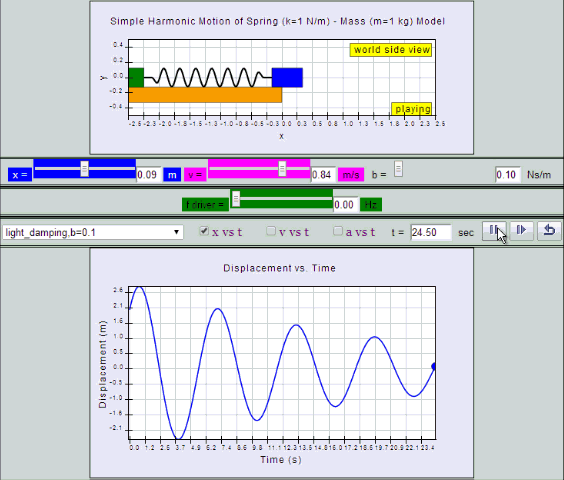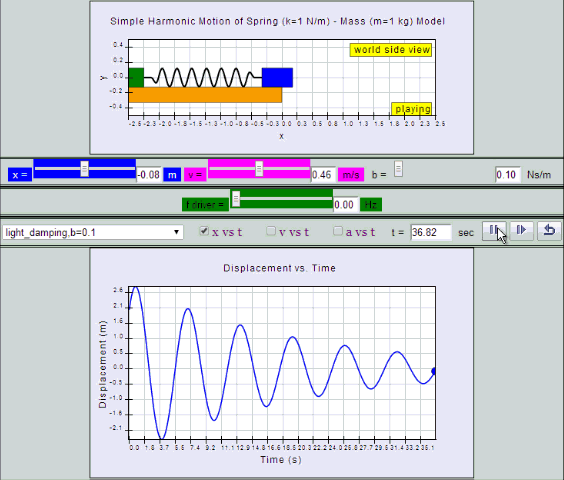
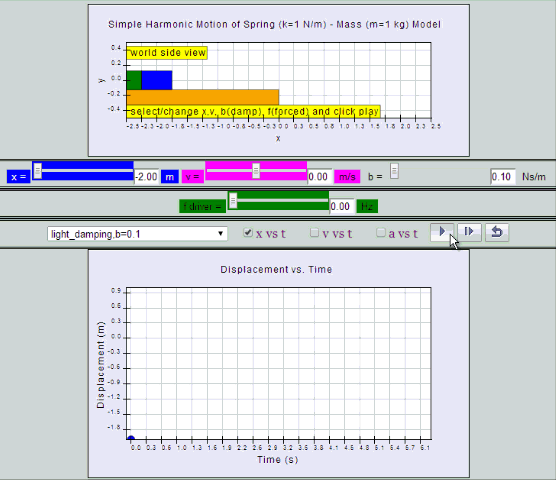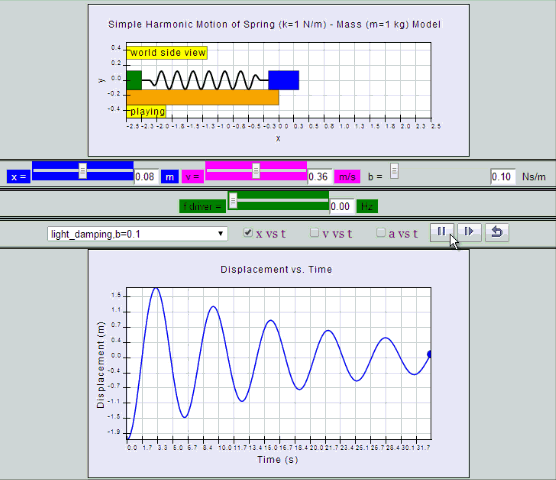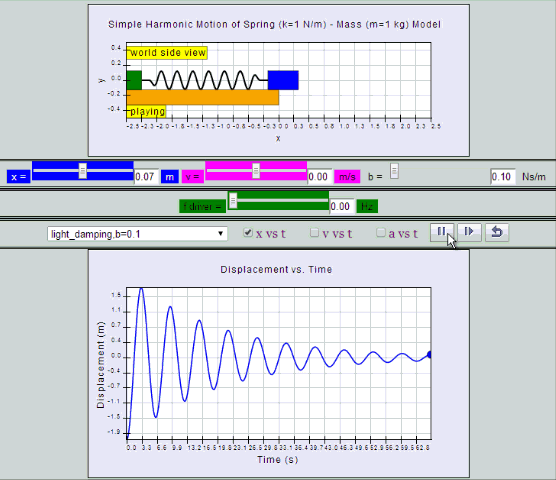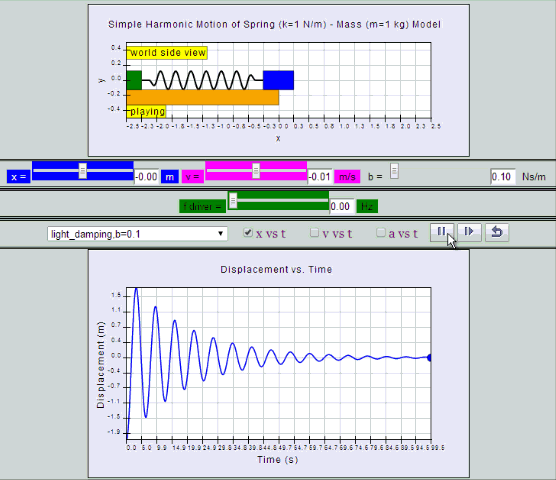
Light Damping:
System undergoes several oscillations of decreasing
amplitude before coming to rest.
 |
| light
damping, b =0.1, SHM starts at equilibrium
position |
 |
| light
damping, b =0.1, SHM starts at position |
 |
| light
damping, b =0.1, SHM starts at position |
Critical Damping
System returns to equilibrium in the minimum time, without
overshooting or oscillating about the equilibrium
position.
Applications of Critical Damping
Car suspension
The spring of a car’s suspension is critically damped so
that when a car goes over a bump, the passenger in the
car quickly and smoothly regains equilibrium.
However, car suspensions are often adjusted to slightly
undercritically damped condition to give a more
comfortable ride. Critical damping also leaves the car
ready to respond to further bumps in the road quickly.
Moving-coil meters
Critical damping is an important feature of moving-coil
meters which are used to measure current and voltage.
When the reading changes, it is of little use if the
pointer oscillates for a while or takes too long to
settle down to the new reading. The new reading must be
taken quickly in case it changes again.
Thus, a pointer is critically damped to allow it to move
to the correct position immediately whenever a current
flows through it or a voltage is applied across it.
Door closers
Devices fitted above doors to prevent slamming.
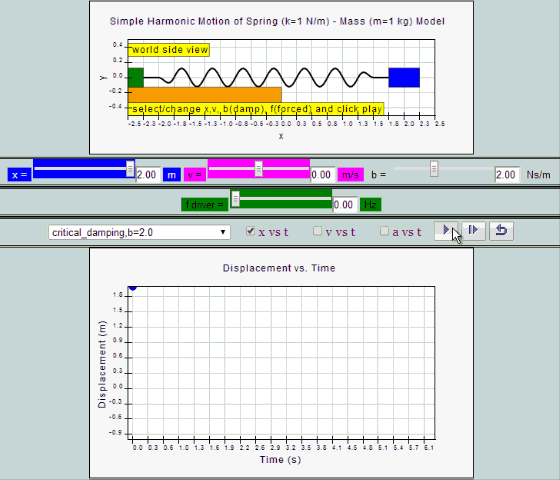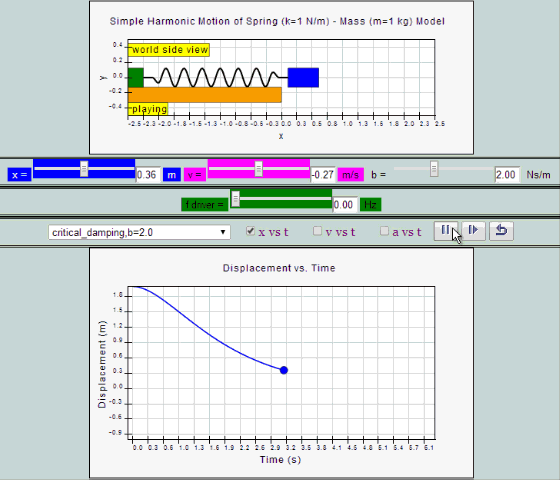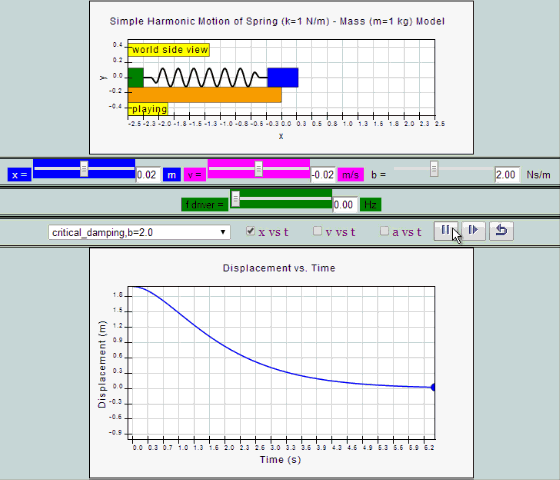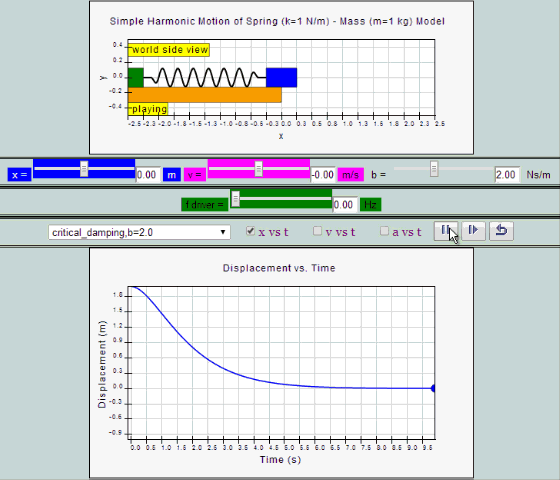 |
| critical
damping, b =2.0 SHM starts at position |
 |
| critical
damping, b =2.0 SHM starts at equilibrium position
|
 |
| critical
damping, b =2.0 SHM starts at position |
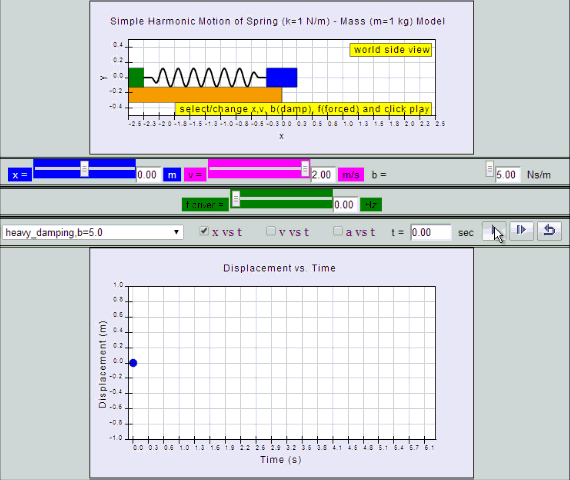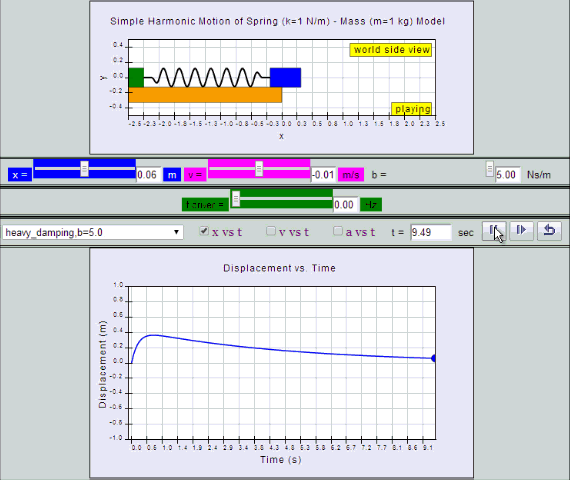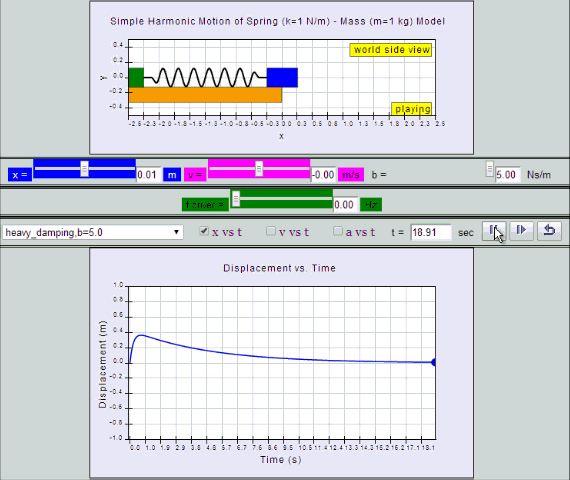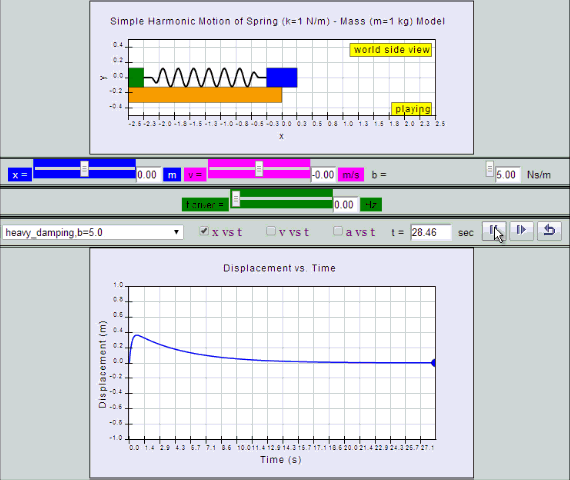
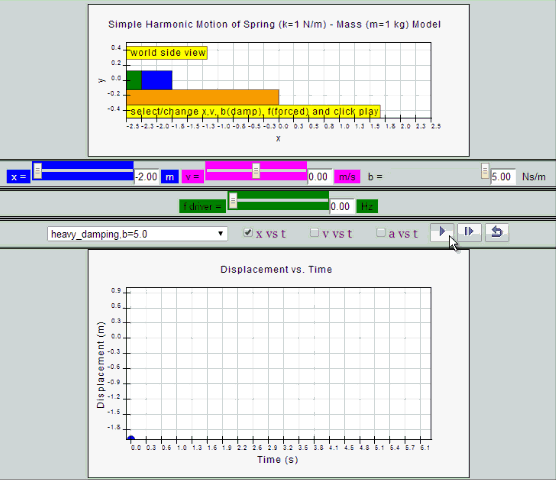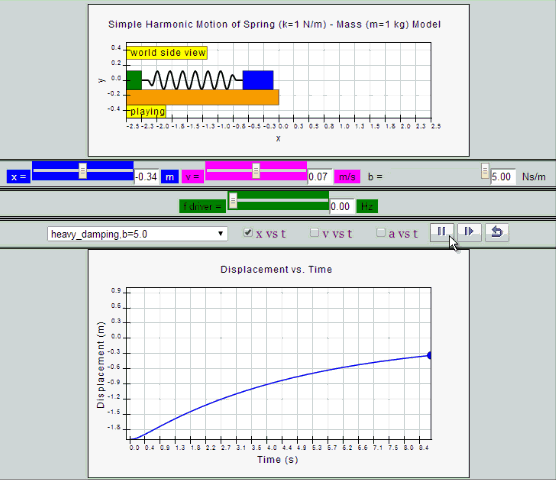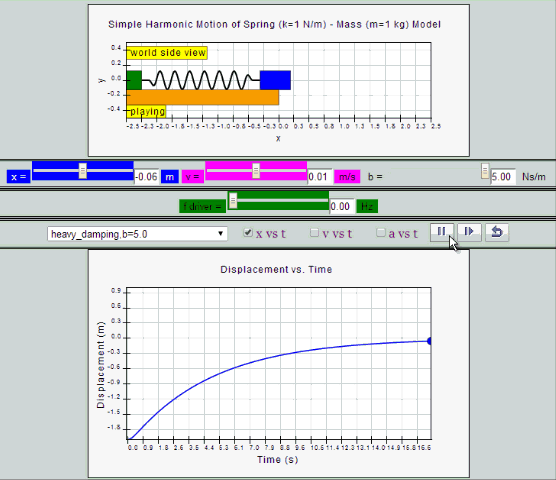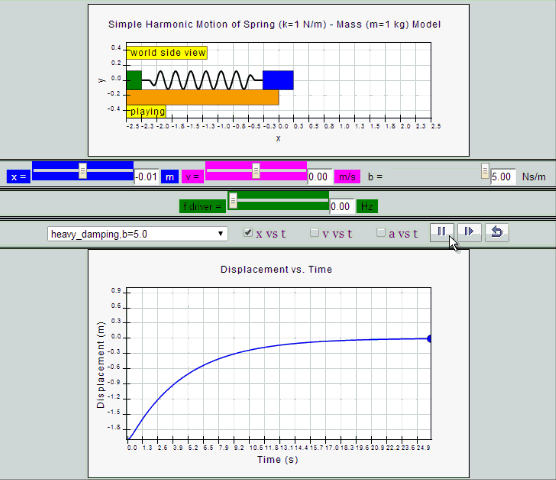
Heavy Damping
System returns to equilibrium very slowly without any
oscillation.
 |
| heavy
damping, b =5.0 SHM starts at equilibrium
position |
 |
| heavy
damping, b =5.0 SHM starts at position |
 |
| heavy
damping, b =5.0 SHM starts at equilibrium
position |