EJSS circle motion to SHM model

EJSS circle motion to SHM model
EJSS simple harmonic motion to circular motion model with phase difference
based on models and ideas by

http://weelookang.blogspot.sg/2014/02/ejss-pendulum-model.html
EJSS circle motion to SHM model
https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMcircle/SHMcircle_Simulation.html
source code: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMcircle.zip
experimental http://phonegap.com/ android app: https://dl.dropboxusercontent.com/u/44365627/EJSScirclemotiontoSHMmodel-debug%20%281%29.apk
author: lookang
author of EJSS 5.0 Francisco Esquembre

Description:

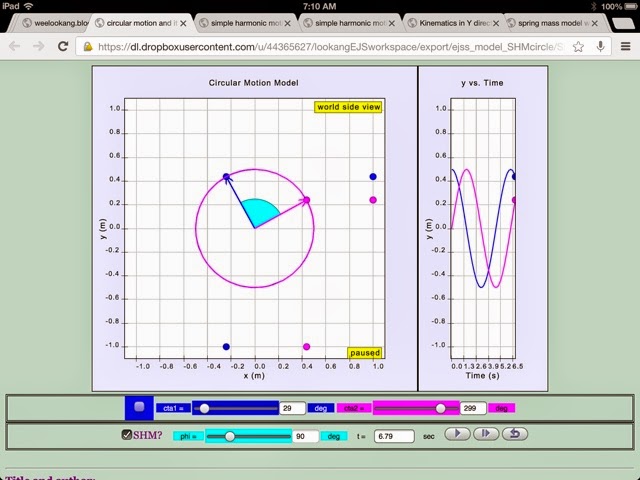
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends on both the body's speed and its direction of travel. This changing velocity indicates the presence of an acceleration; this centripetal acceleration is of constant magnitude and directed at all times towards the axis of rotation. This acceleration is, in turn, is responsible for a centripetal force which is also constant in magnitude and directed towards the axis of rotation.

The equations that model the motion of the circular motion are:

this uniform

ω1 =

ω2 circular motion model assumes

δθ1δt=ω1

δθ2δt=ω2

where the terms

θ1 and

θ2 represents the angle of rotation in uniform circular motion

ω1 and

ω2 are constants equal to each other.
in circular motion,

θ1=ω1t

θ2=ω2t

results in phase difference of

ϕ=θ1−θ2 when rotation is clockwise

ϕ=θ2−θ1 when rotation is anti-clockwise viewed from your perspective.

Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular speed

ω around a circle of radius

A centered at the origin of the

x−y plane, then its motion along each coordinate is simple harmonic motion with amplitude

A and angular frequency

ω.

The simplified equations that model the motion projection of circular motion = simple harmonic motion are:

y1=A1cos(ω1t)

then

y2=A2cos(ω2t−ϕ)

and

x1=−A1sin(ω1t)

then

x2=A2sin(ω2t+ϕ)