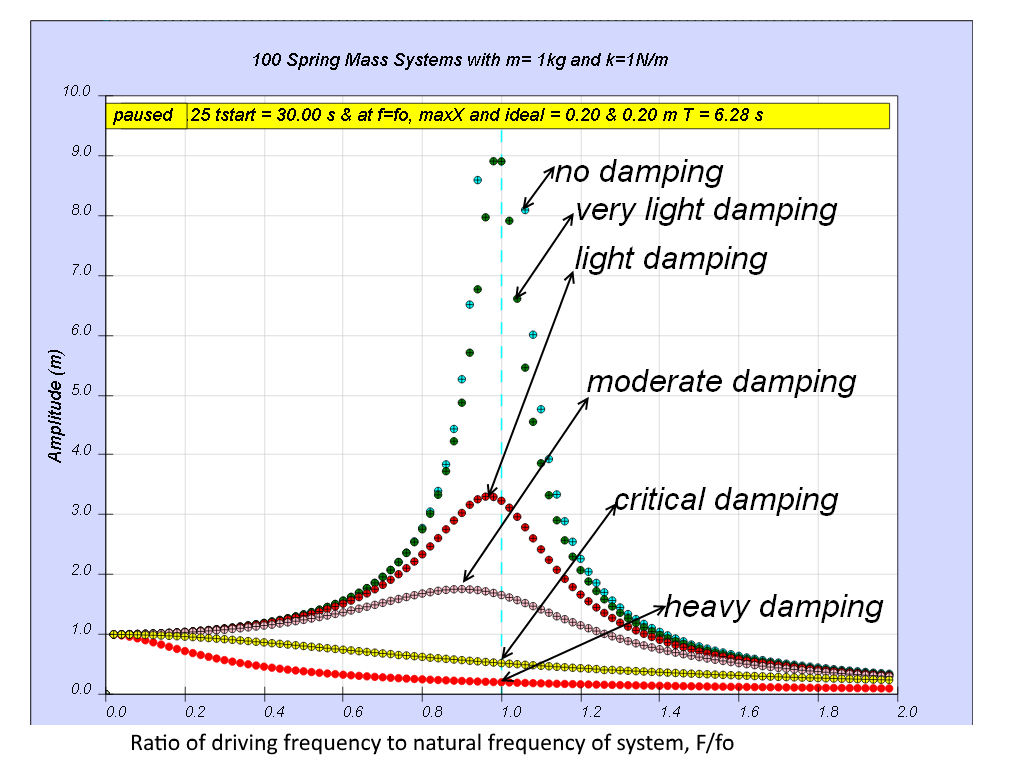
When the driving frequency f is close to or equal to the natural frequency fo of the oscillating system, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude. This phenomenon is called resonance.
A more accurate and complicated picture could be found on Wikipedia.
This computer model can be used to generate a similar data representation when using the instruction found on the html below the model.

Case: b=0 no damping.
All 100 spring mass systems oscillates forever without coming to rest. Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo = 1 maximum energy is transferredfrom the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (extended beyond 10). This phenomenon is called resonance.
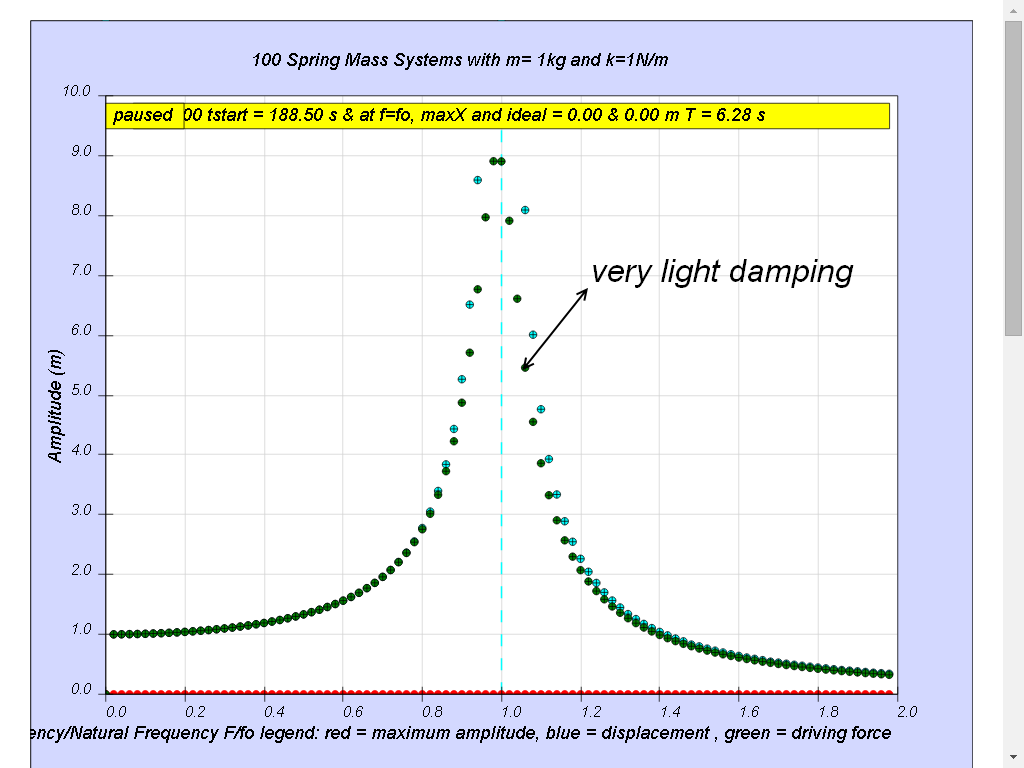
Case 1: b=0.1 very light damping
Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo = 1 maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (equal 10 m). This phenomenon is called resonance.
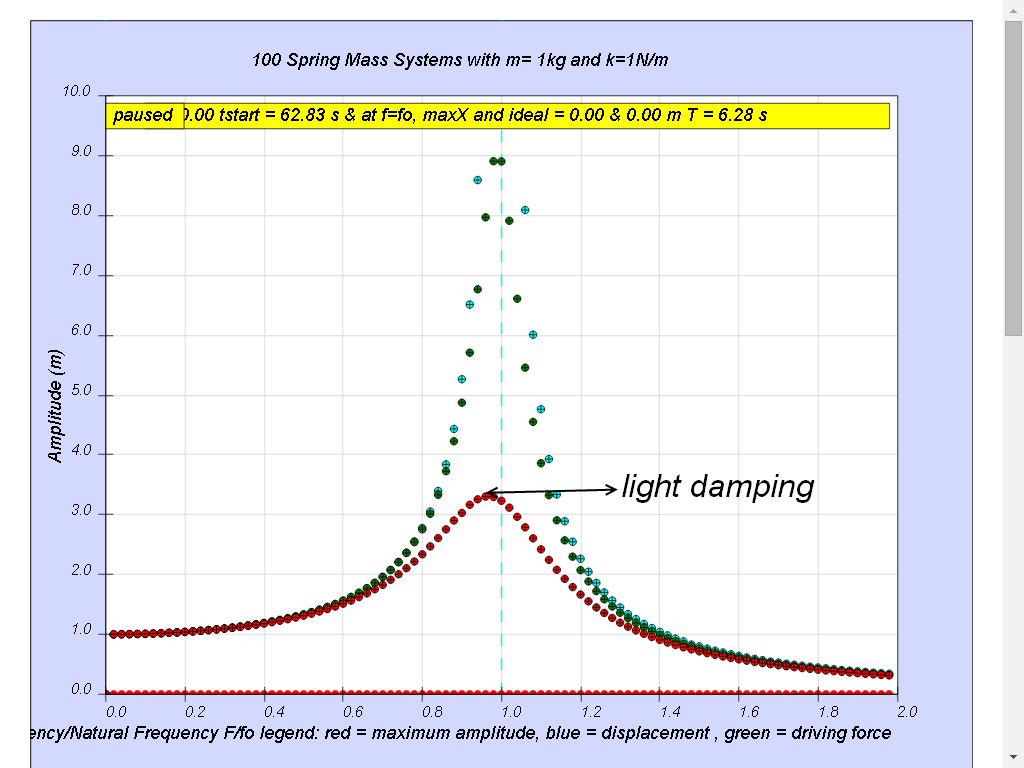
Case2: b=0.3 light damping
Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo slightly less than 1, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 3.3). This phenomenon is called resonance.
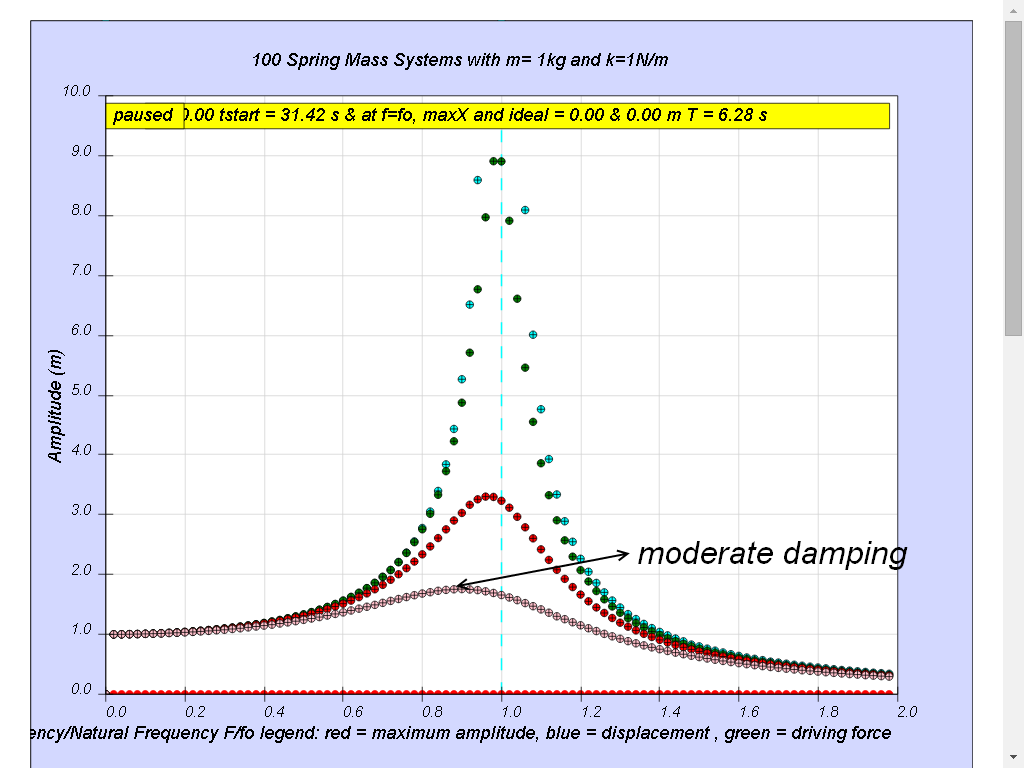
Case3: b =0.6 moderate damping
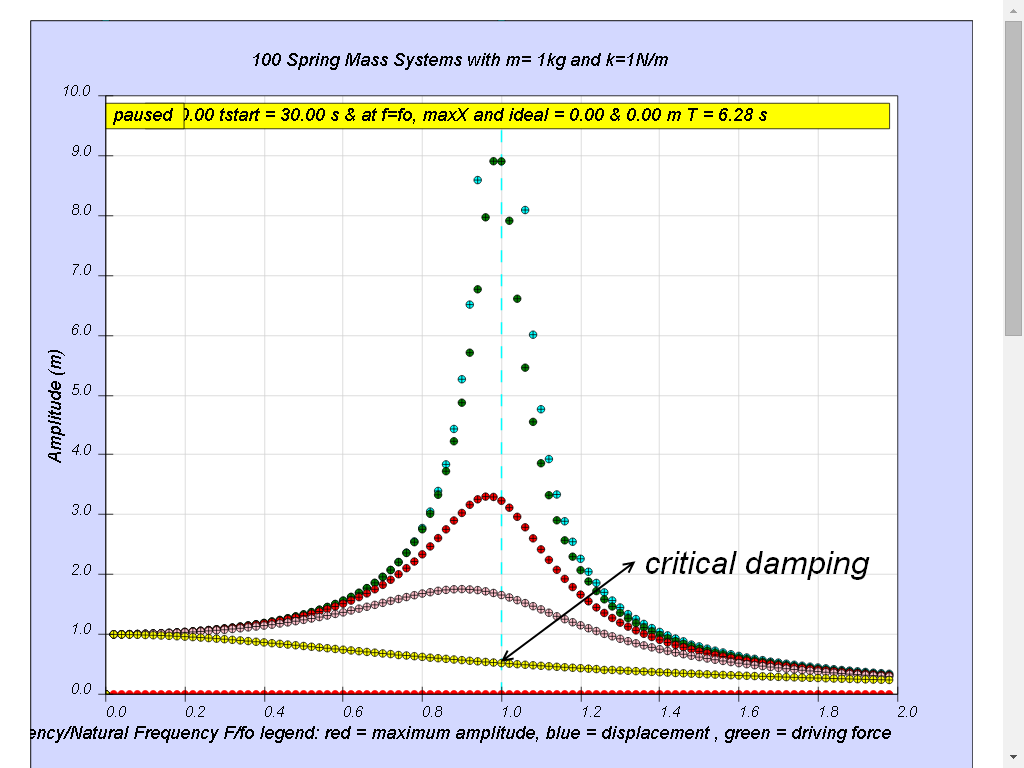
Notice when the ratio of driving frequency to natural frequency fo of the oscillating system f/fo slightly less than 1 about 0.9 in this case, maximum energy is transferred from the periodic force (driver) to the oscillating system which will vibrate with maximum amplitude (about 1.8). This phenomenon is called resonance.
Case4: b = 2.0 critical damping
Notice the resonance does not occur anymore.
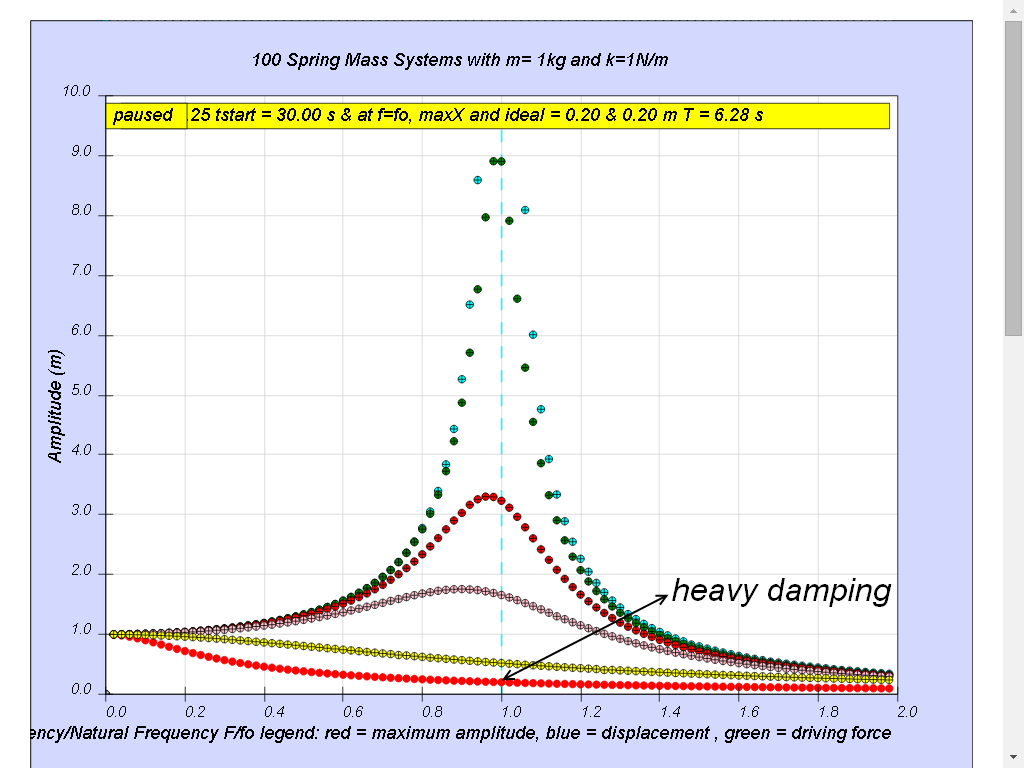
Case5: very heavy damping
Notice the resonance does not occur anymore.
http://youtu.be/LV_UuzEznHs How is this video related to resonance? Hint: consider the shaking support table is the driver, moving an driver frequency f, and the natural frequency of the left, middle and right structure each have their own natural frequency f01, f02, f03.
http://youtu.be/17tqXgvCN0E This video shows the oscillating of a wine glass by playing sound (driver) at its(wine glass) natural frequency resulting in resonance.Note stroboscope is used to observe the resonant effect better.
http://youtu.be/M8ztJGT6AHc Marina Bay Sands
cantilever - real world application of resonance.
Note that video ends at 5.40 min.
http://youtu.be/1yaqUI4b974 Though not really in A-Level Physics syllabus, the experiment shows the beauty of physics where sound at certain frequencies can produce detailed 2 dimensions patterns of sands that tends to be deposited at positions where the displacement is zero and areas of resonances (high amplitudes) the sand tend to be disturbed and move away from these position, resulting in the detailed patterns of sands.