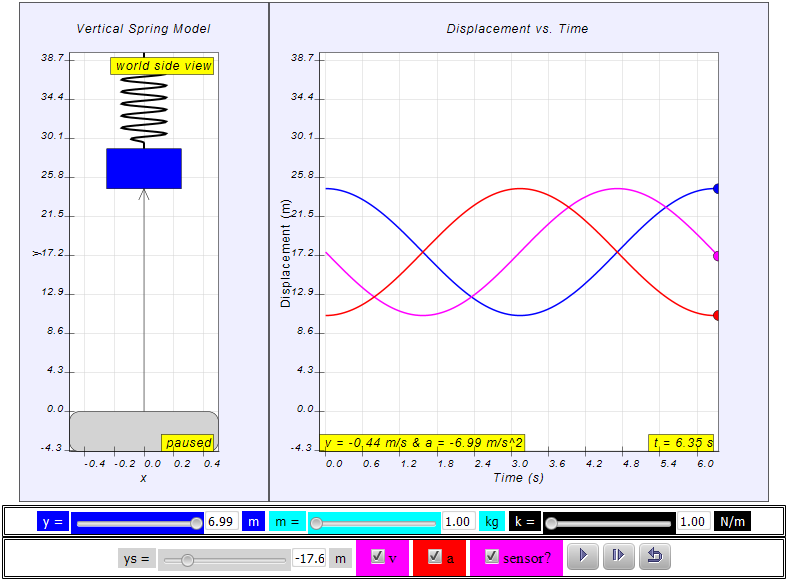
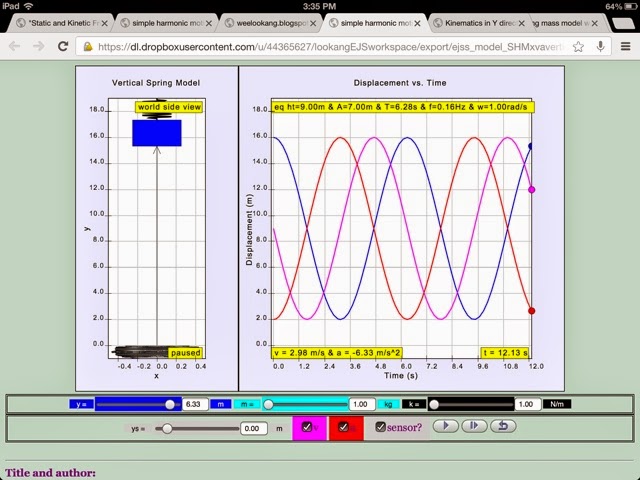
EJSS simple harmonic motion vertical spring mass model with sensor
based on models and ideas by
- lookang http://weelookang.blogspot.sg/2014/02/ejss-shm-model-with-vs-x-and-v-vs-x.html
- lookang http://weelookang.blogspot.sg/2010/06/ejs-open-source-simple-harmonic-motion.html?q=SHM
- lookang http://weelookang.blogspot.sg/2013/02/ejs-open-source-vertical-spring-mass.html?q=vertical+spring
- Wolfgang Christian and Francisco Esquembre http://www.opensourcephysics.org/items/detail.cfm?ID=13103
Assumption:
Motion approximates SHM when the spring does not exceed limit of proportionality during oscillations. |
| http://weelookang.blogspot.com/2014/02/ejss-vertical-spring-mass-model.html EJSS SHM vertical spring mass model with y vs t, v vs t and a vs t graph suitable for understanding lowering equilibrium position effects of mass m https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMxvavertical/SHMxvavertical_Simulation.html source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMxvavertical.zip author: lookang author of EJSS 5.0 Francisco Esquembre |
The equations that model the motion of the vertical spring mass system are:
where F is
the restoring elastic force exerted by the spring (in SI
units: N),
k
is the spring
constant (N·m−1),
and y
is the displacement
from the equilibrium position (in m).
δyδt=vy
δvyδt=−km(y)
where the terms
−km(y) represents the restoring
force component as a result of the spring extending and
compressing.
Why is the equation
josh explains it well here
In equilibrium position,
−kye−mg=0
ye=−mgk
−ky0−mg=ma
where $ y_{0} is the new position or length extra extended beyond the natural length
−ky0−(−kye)=ma
−k(y0−ye)=ma
−ky=ma
which keeps the equilibrium constantly at zero and the massm
and spring constant k
effects the angular frequency ω=(km)−−−−√ .
So gravity has no effect on the oscillation frequency ω .
h=ysensor
Thus, this model is simplified by http://physics.ucsc.edu/~josh/6A/book/harmonic/node13.html
assumes
where the terms
Why is the equation −ky=ma
?
josh explains it well hereIn equilibrium position,
where $ y_{e} is the position or length extended beyond
the natural length
using Fnet=ma
where $ y_{0} is the new position or length extra extended beyond the natural length
renaming (y0−ye)
as y
we get
which keeps the equilibrium constantly at zero and the mass
Calculations used in the model:
Equilibrium height or position h :
typically it is zero but it may be displaced with a
different origin thus using this equation helps
Amplitude x0
is defined as magnitude of the maximum displacement from the
equilibrium position. Since the motion starts when zero initial velocity, it is generally true that
x0=y
when t=0
PeriodT
Time taken for one complete oscillation is easily to
determined visually but it can be a challenge to
pre-determined even before the model runs t=0 .
The way used in the model is to determine period by
assuming
T=2πmk−−√
f=1T
Angular Frequencyω
is the about of angle in radian covered per unit time.
Thus, if knowing T
is the time for one complete oscillation which is 2π
radians, thus
ω=2πT=2πf
equilibrium position. Since the motion starts when zero initial velocity, it is generally true that
Period
Frequency f
Number of oscillations performed per unit time.
Mathematically the period is related to frequency as a
reciprocal of the other.
Angular Frequency