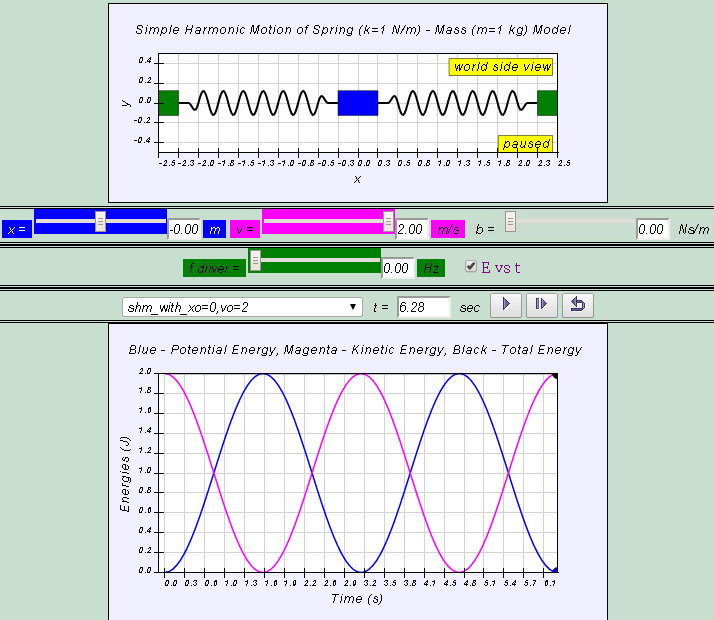
EJSS simple harmonic motion model with energy vs t graph showing elastic potential, kinetic and total energy
based on models and ideas by
- lookang http://weelookang.blogspot.sg/2010/06/ejs-open-source-simple-harmonic-motion.html?q=SHM
- Wolfgang Christian and Francisco Esquembre http://www.opensourcephysics.org/items/detail.cfm?ID=13103
 |
| http://weelookang.blogspot.sg/2014/02/ejss-shm-e-vs-t.html EJSS simple harmonic motion model with energy vs t graph showing elastic potential, kinetic and total energy https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMet/SHMet_Simulation.html source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMet.zip author: lookang author of EJSS 5.0 Francisco Esquembre |
notes:
 |
| http://weelookang.blogspot.sg/2014/02/ejss-shm-e-vs-t.html EJSS simple harmonic motion model with energy vs t graph showing elastic potential, kinetic and total energy https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMet/SHMet_Simulation.html source: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMet.zip author: lookang author of EJSS 5.0 Francisco Esquembre |
The equations that model the motion of the spring mass system are:
where F is
the restoring elastic force exerted by the spring (in SI
units: N),
k is the spring
constant (N·m−1),
and x is the displacement
from the equilibrium position (in m).
δxδt=vx
δvxδt=−km(x−l)−bvxm+Asin(2πft)m
where the terms
−km(x−l) represents the restoring
force component as a result of the spring extending and
compressing.
−bvxm represents the damping
force component as a result of drag retarding the mass's
motion.
+Asin(2πft)m
represents the
driving force component as a result of a external periodic
force acting the mass m .
Once the mass is displaced from its equilibrium position, it
experiences a net restoring force. As a result, it accelerates
and starts going back to the equilibrium position. When the
mass moves closer to the equilibrium position, the restoring
force decreases. At the equilibrium position, the net
restoring force vanishes. However, at x = 0, the mass has momentum
because of the impulse
that the restoring force has imparted. Therefore, the mass
continues past the equilibrium position, compressing the
spring. A net restoring force then tends to slow it down,
until its velocity
reaches zero, whereby it will attempt to reach equilibrium
position again.
As long as the system has no energy loss, the mass will continue to oscillate. Thus, simple harmonic motion is a type of periodic motion.
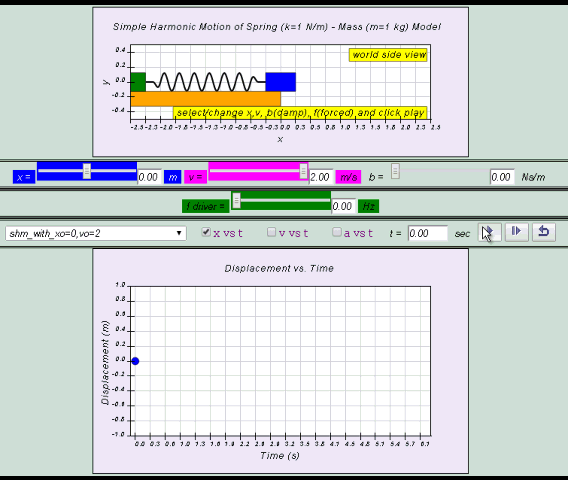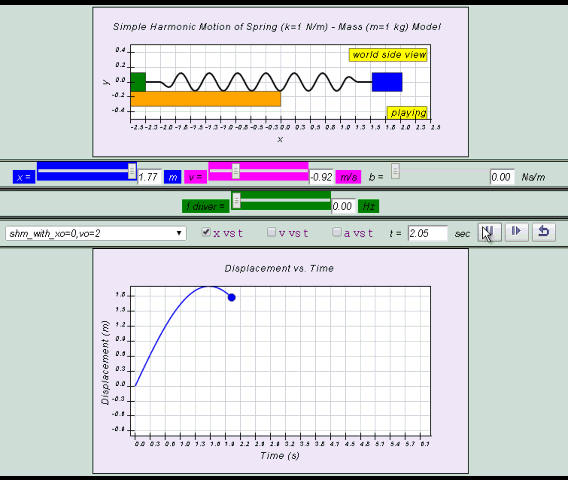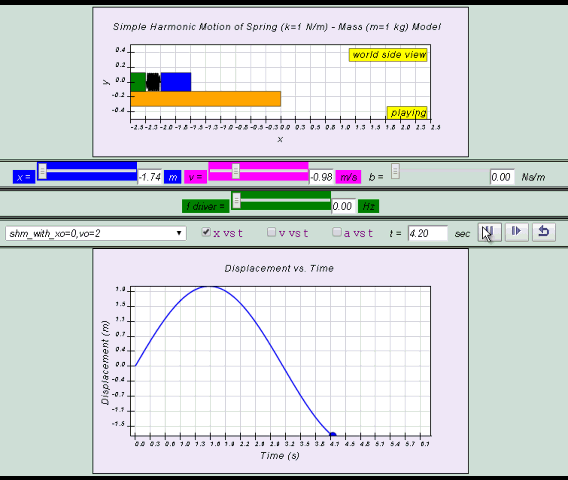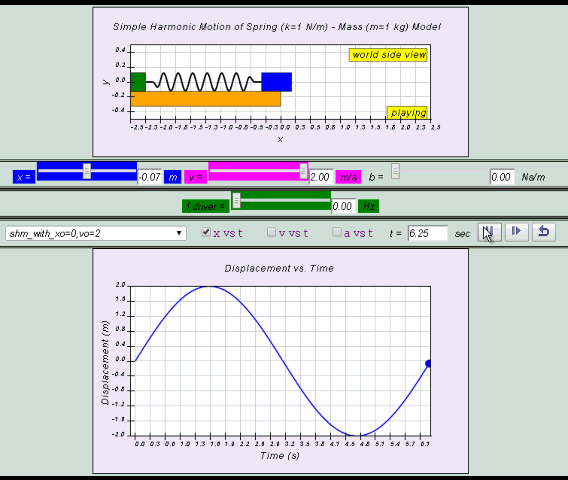
At the time of release, the energy of the system will consist totally of the spring’s potential energy. As the spring pulls the mass toward the equilibrium position, the potential energy is transformed into kinetic energy until at the equilibrium position the kinetic energy will reach a maximum. After the mass crosses the equilibrium position, the spring is compressed and the EP is converted to EK. Maximum PE occurs at maximum compression of spring.
The constant exchange between potential energy EP and kinetic energy EK is essential in producing oscillations. The total energy ET, which is the summation of kinetic and potential energy, will always add up to a constant value as shown.
Variation with time of energy in simple harmonic motion are as follows:
KE=12mv2=12mω2x2ocos2(ωt)
PE=12kx2=12mω2x2osin2(ωt)
TE=KE+PE=12mω2x2o
x=−xocos(ωt)=xosin(ωt−π2)
v=xoωsin(ωt)=xoωcos(ωt−π2)
a=xoω2cos(ωt)=−xoω2sin(ωt−π2)
KE=12mv2=12mω2x2osin2(ωt)
PE=12kx2=12mω2x2ocos2(ωt)
TE=KE+PE=12mω2x2o
therefore , in general:
x=xosin(ωt−ϕ)
v=xoωcos(ωt−ϕ)
a=−xoω2sin(ωt−ϕ)
KE=12mv2=12mω2x2ocos2(ωt−ϕ)
PE=12kx2=12mω2x2osin2(ωt−ϕ)
TE=KE+PE=12mω2x2o
Thus, this model assumes
where the terms
What is SHM?
Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. In order for simple harmonic motion to take place, the net force of the object at the end of the pendulum must be proportional to the displacement. In other words, oscillations are periodic variations in the value of a physical quantity about a central or equilibrium value.As long as the system has no energy loss, the mass will continue to oscillate. Thus, simple harmonic motion is a type of periodic motion.
Energy of SHM:
Consider a spring of spring constant k connected to a
mass m as shown. When the mass is displaced from
its equilibrium position by a distance xo and released,
it will oscillate backwards and forwards
At the time of release, the energy of the system will consist totally of the spring’s potential energy. As the spring pulls the mass toward the equilibrium position, the potential energy is transformed into kinetic energy until at the equilibrium position the kinetic energy will reach a maximum. After the mass crosses the equilibrium position, the spring is compressed and the EP is converted to EK. Maximum PE occurs at maximum compression of spring.
The constant exchange between potential energy EP and kinetic energy EK is essential in producing oscillations. The total energy ET, which is the summation of kinetic and potential energy, will always add up to a constant value as shown.
Variation with time of energy in simple harmonic motion are as follows:
If motion starts at the equilibrium position and starts to move to the positive direction solutions to the defining equation are:
 |
| spring mass system in SHM where
|
If the motion starts to the negative amplitude position:
 |
| motion
starts at the negative position and starts to
move to the positive direction, defining
equation follows |
 |
| motion
starts at the negative position and starts to
move to the positive direction, defining
equation follows |
 |
| motion
starts at the negative position and starts to
move to the positive direction, defining
equation follows |
therefore , in general: