EJSS simple harmonic motion to circular motion model with phase difference
based on models and ideas by
 |
| http://weelookang.blogspot.sg/2014/02/ejss-pendulum-model.html EJSS circle motion to SHM model https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMcircle/SHMcircle_Simulation.html source code: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMcircle.zip experimental http://phonegap.com/ android app: https://dl.dropboxusercontent.com/u/44365627/EJSScirclemotiontoSHMmodel-debug%20%281%29.apk author: lookang author of EJSS 5.0 Francisco Esquembre |
- lookang http://weelookang.blogspot.sg/2012/07/ejs-open-source-phase-difference-java.html
- lookang http://weelookang.blogspot.sg/2013/02/ejs-open-source-vertical-spring-mass.html?q=vertical+spring
 |
| http://weelookang.blogspot.sg/2014/02/ejss-pendulum-model.html EJSS circle motion to SHM model https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHMcircle/SHMcircle_Simulation.html source code: https://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_src_SHMcircle.zip experimental http://phonegap.com/ android app: https://dl.dropboxusercontent.com/u/44365627/EJSScirclemotiontoSHMmodel-debug%20%281%29.apk author: lookang author of EJSS 5.0 Francisco Esquembre |
Description:
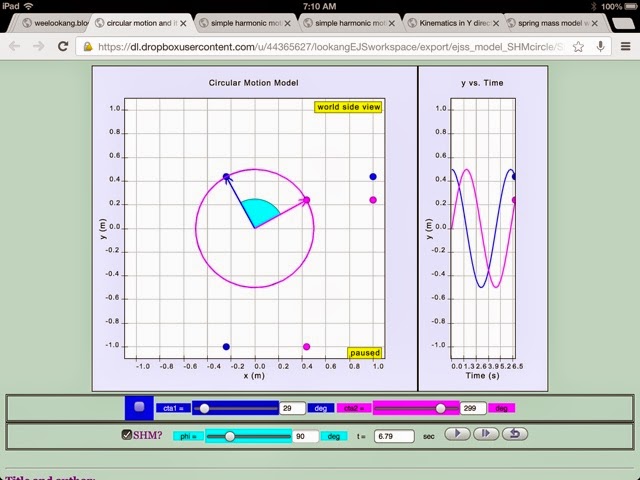
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends on both the body's speed and its direction of travel. This changing velocity indicates the presence of an acceleration; this centripetal acceleration is of constant magnitude and directed at all times towards the axis of rotation. This acceleration is, in turn, is responsible for a centripetal force which is also constant in magnitude and directed towards the axis of rotation.The equations that model the motion of the circular motion are:
where the terms
θ1
and θ2
represents the angle of rotation in uniform circular motion
ω1
and ω2
are constants equal to each other.
in circular motion,
θ1=ω1t
θ2=ω2t
ϕ=θ1−θ2
when rotation is clockwise
in circular motion,
results in phase difference of
Simple harmonic motion can in some cases be considered to be
the one-dimensional projection
of uniform
circular motion. If an object moves with angular speed
ω
around a circle of radius A
centered at the origin
of the x−y
plane, then its motion along each coordinate is simple
harmonic motion with amplitude A
and angular frequency ω .
and
The simplified equations that model the motion projection of circular motion = simple harmonic motion are:
if y1=A1cos(ω1t)
then y2=A2cos(ω2t−ϕ)
and
if x1=−A1sin(ω1t)
then x2=A2sin(ω2t+ϕ)