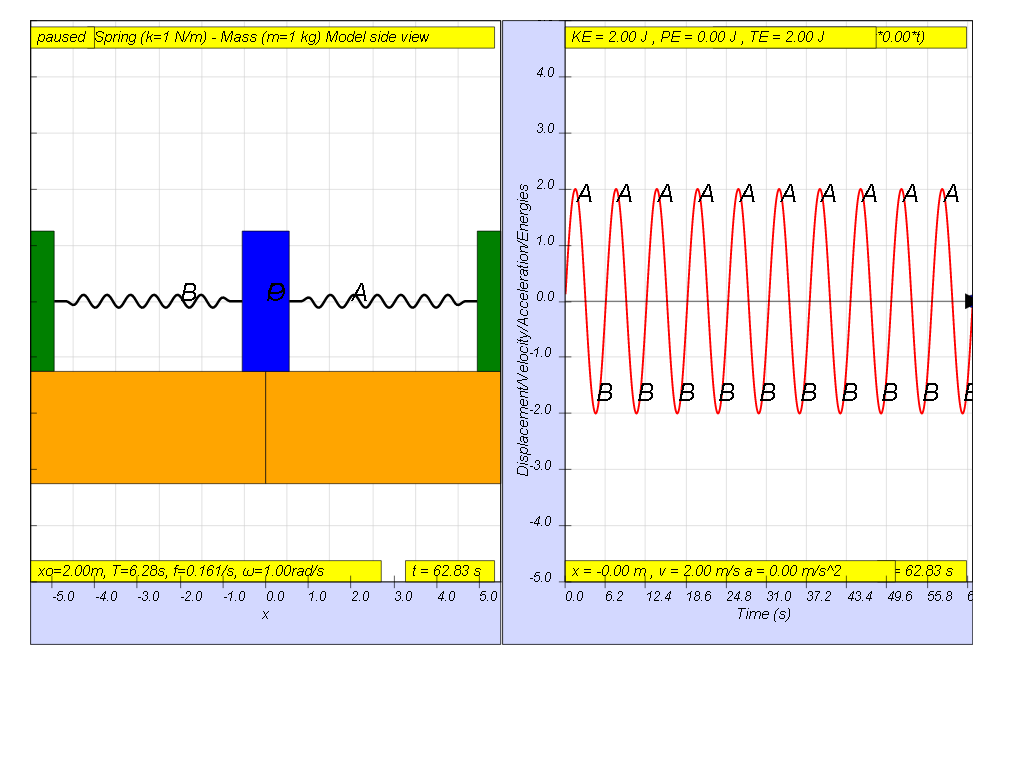
When a system performs oscillations without any applied force, the frequency of the oscillation is a characteristic of the system and is called the natural frequency, fo . In the example above, the fo = 0.161 Hz.

When a system performs oscillations without any applied force, the
frequency of the oscillation is a characteristic of the system and
is called the natural frequency, fo . In the
example above, the fo = 0.161 Hz.
Consider a spring mass system initially at rest.
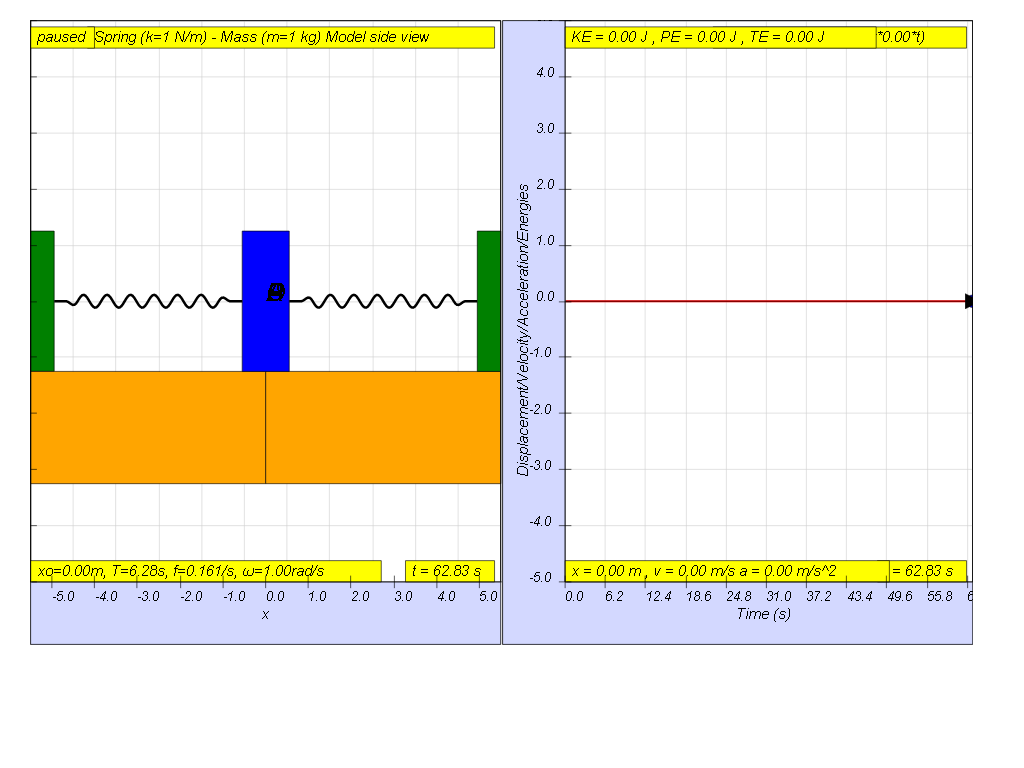
When the driving force is at f = 0, that means the driving force is Fdriver = (0.5)sin(2π f t ) = 0.
the result is as shown on the picture where x = 0 for all time since there is no external driving force acting on the system.
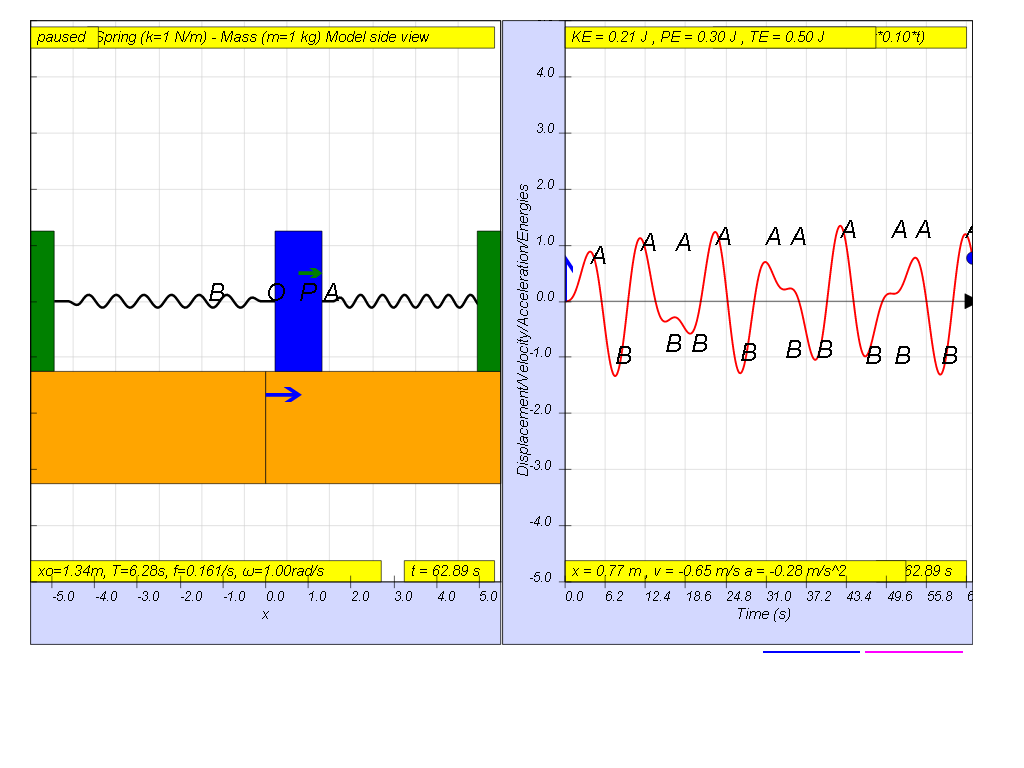
However, when f = 0.1 , the Fdriver = (0.5)sin(2π (0.1) t ), it results in a motion that seems to irregular reaching a maximum amplitude of A and B (see picture).
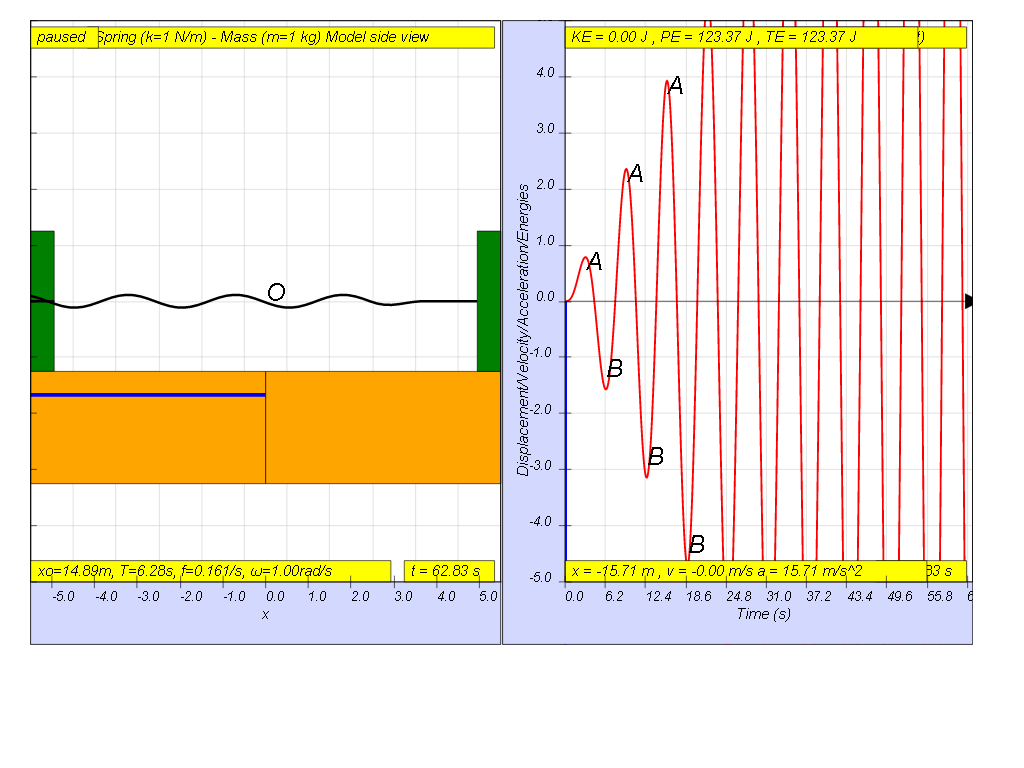
However, when f = 0.159 , the Fdriver = (0.5)sin(2π (0.159) t ), it results in a motion that seems to increase to a very large maximum amplitude of A and B (see picture, when t = 55.8, A and B are greater than the screen display height). Theoretically, is should be infinitely large.
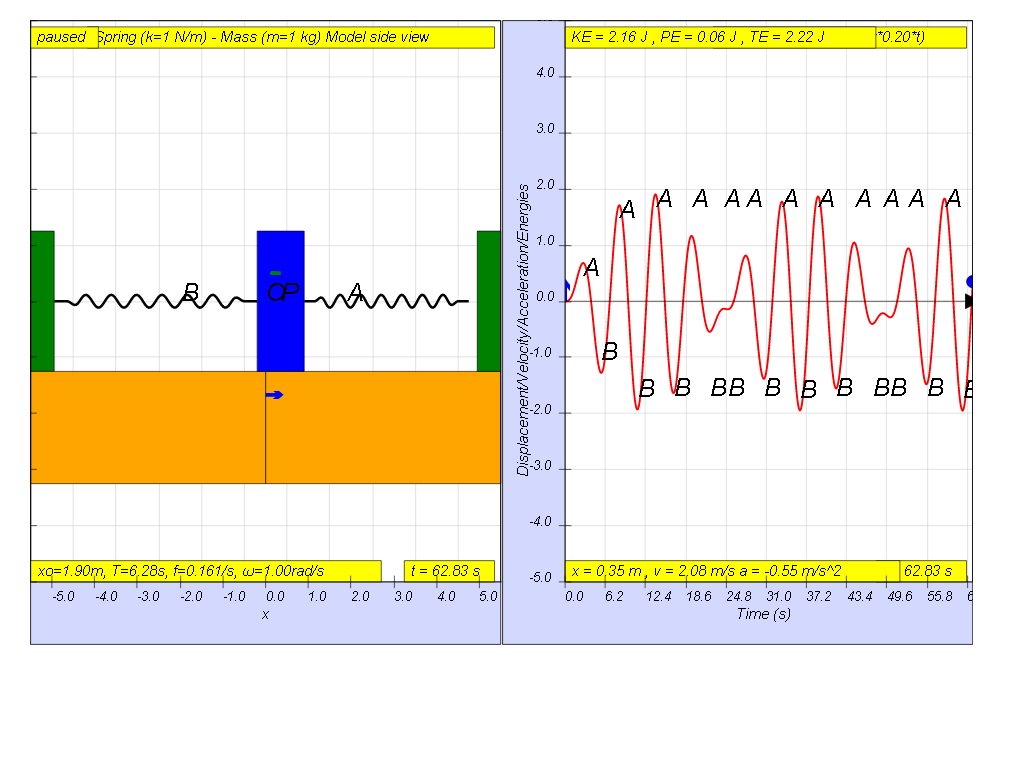
However, when f = 0.2 , the Fdriver = (0.5)sin(2π (0.2) t ), it results in a motion that seems to also reach some smaller maximum amplitude of A and B (see picture reaching about 1.8 ).
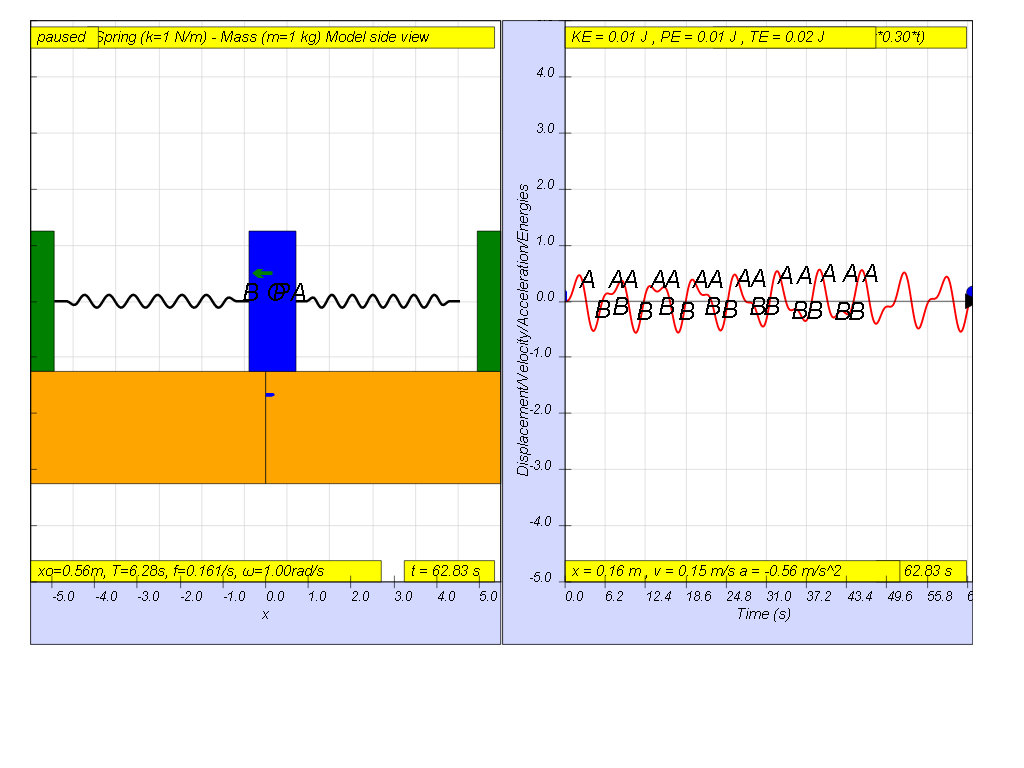
However, when f = 0.3 , the Fdriver = (0.5)sin(2π (0.3) t ), it results in a motion that seems to also reach rather maximum amplitude of A and B (see picture reaching about 0.5 ).
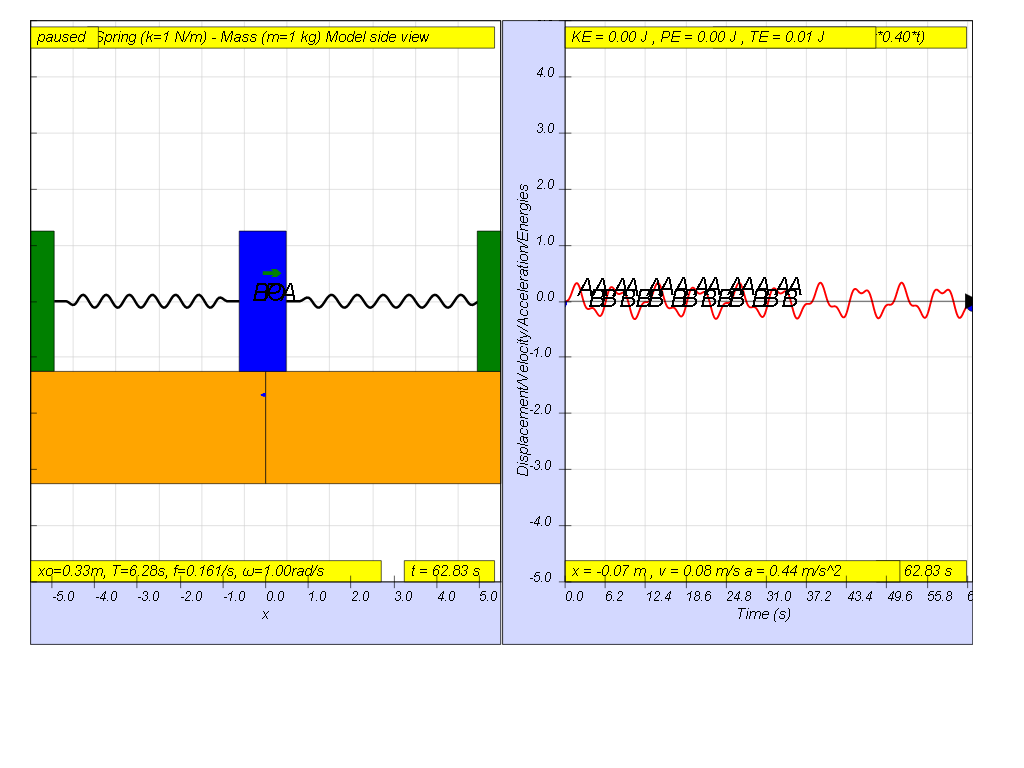
Lastly, when f = 0.4 , the Fdriver = (0.5)sin(2π (0.4) t ), it results in a motion that seems to also reach even smaller maximum amplitude of A and B (see picture reaching about 0.3 ).
These oscillations in which a periodic force is imposed are called forced resonance. Systems will then some what influenced to vibrate at the frequency of the periodic force, f, but only when f = fo = 0.161 Hz , in this example, the maximum amplitude is the greatest happens in this case when damping is zero as has similar maximum amplitude effects for different damping levels occurring near f = fo
1)
Vibrations of a pendulum clock.
2) Vibrations of a tuning fork when exposed to
the periodic force of a sound wave.
3) Vibration of a bridge under the influence of
marching soldiers or periodic wind.