Example
A body moves in a simple harmonic motion and the following graph
gives the variation of its displacement x with time t.
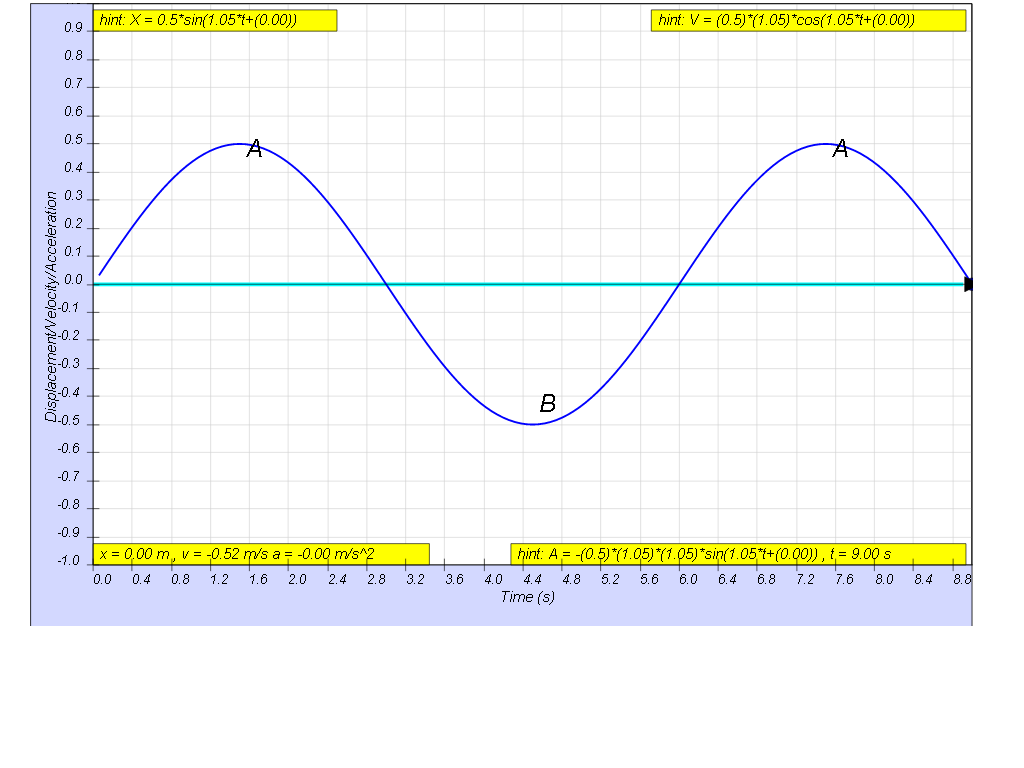
a) Write an equation to represent the given
simple harmonic motion.
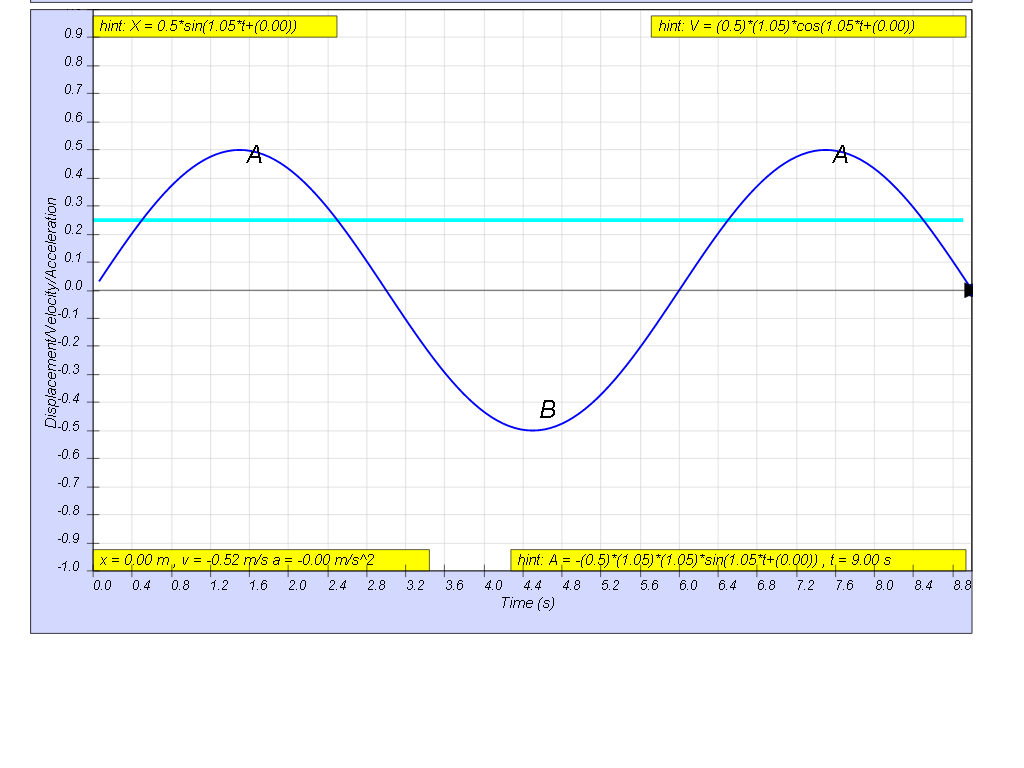
b) Find the time duration in the first cycle
when the body is located above a displacement of 0.25 m.
[ x = xo sin (1.05 t) , Δt =
1.9 s ]
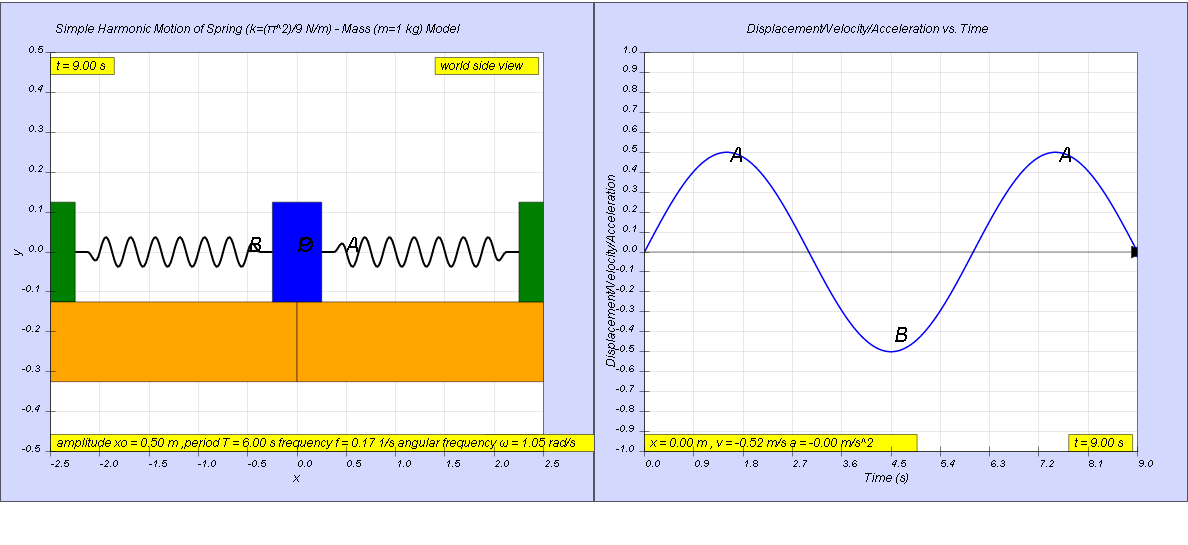
The
hint can be found in the model
Solution:
a) x0 = 0.5 m
ω = 1.05
x = x0sin(ω t) = 0.5 sin(1.05t)
b) At x = 0.25 m,
substituting back into the equation,
0.25 = 0.5 sin(1.05t)
solving for t gives
0.5 = sin(1.05t)
solving of the ranging of time, t
1.05t = 0.524 and π - 0.524
t1 =
0.5 , t2 = 2.4 s
looking at the graphical form of the
solution of the 2 times, t1 and
t2.
giving the range to be t2 - t1 = 2.4 -
1.5 = 1.9 s
Model:
http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM13/SHM13_Simulation.xhtml


