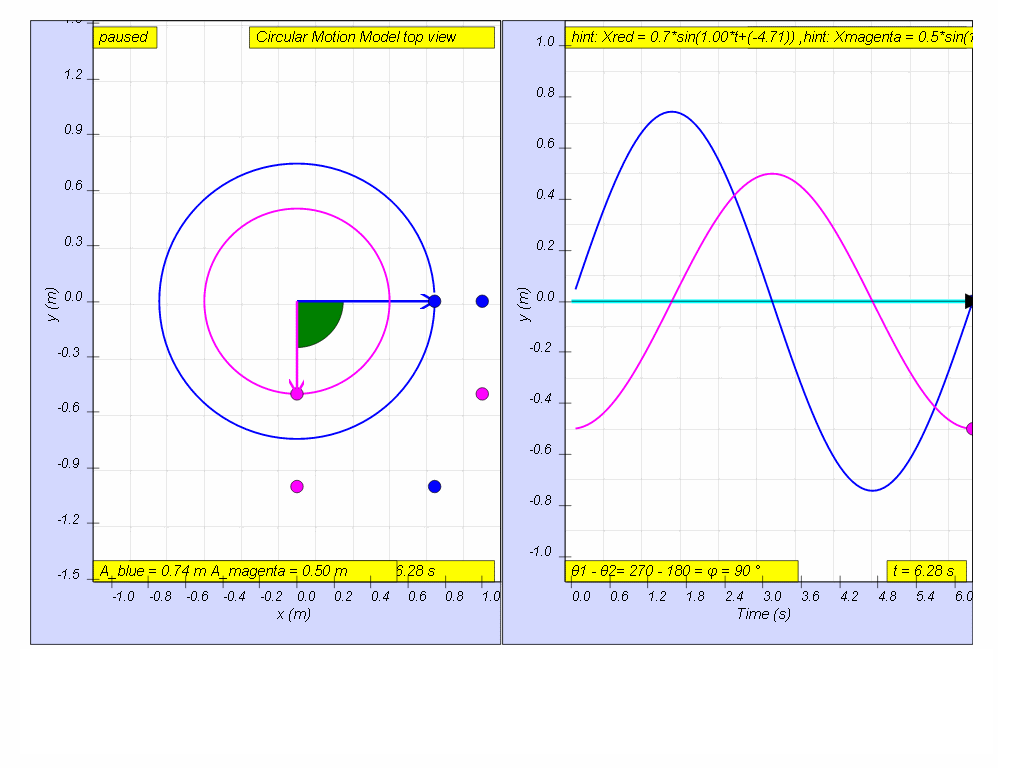
Simple
harmonic motion can in some cases be considered to be the
one-dimensional projection of uniform circular motion. If an
object moves with angular speed ω around a circle of radius A
centered at the origin of the x−y plane,
then its motion along each coordinate is simple harmonic motion
with amplitude A and angular frequency ω.

A1: y = Asin (ωt)
A2: y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position
A3: both x = A cos(ω t) and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of and respectively.
http://youtu.be/0IaKcqRw_Ts This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion.